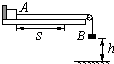题目内容
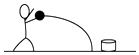
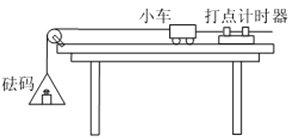
【题目】如图1所示，轻质弹簧原长为2L，将弹簧竖直放置在水平地面上，在其顶端将一质量为5m的物体由静止释放，当弹簧被压缩到最短时，弹簧长度为L．现将该弹簧水平放置（如图2所示，弹簧图略缩小），一端固定在A点，另一端与物块P接触但不连接．AB是长度为5L的水平轨道，B端与半径为L的光滑半圆轨道BCD相切，半圆的直径BD在竖直方向上，如图所示．物块P与AB间的动摩擦因数μ=0.5．用外力推动物块P，将弹簧压缩至长度为L处，然后释放P，P开始沿轨道运动，重力加速度为g．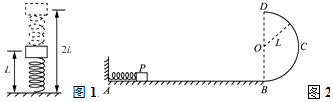
（1）求当弹簧压缩至长度为三时的弹性势能Ep；
（2）若P的质量为m，求物体离开圆轨道后落至AB上的位置与B点之间的距离s；
（3）为使物块P滑上圆轨道后又能沿圆轨道滑回，求物块P的质量取值范围．
【答案】
（1）
解：由机械能守恒定律知，弹簧长度为L时的弹性势能为EP，
所以有：EP=5mgL
（2）
解：设P到达B点时的速度大小为vB，由能量守恒定律得：EP= 
mvB2+μmg（5L﹣L）
代入数据解得：vB= 
设P滑到D点时的速度为vD，由机械能守恒定律得： mvB2= mvD2+2mgL
解得：vD= 
物体从D点以速度vD水平射出，设P落回到轨道AB所需时间为t
竖直方向上：2L= gt2
水平方向上：s=vDt
联立解得：s=2 
（3）
解：设P的质量为M，为使P能滑上圆轨道，它到达B点时的速度不能小于0，
则有：5mgL＞4μMgL
要使P仍能沿圆轨道滑回，P在圆轨道的上升高度不能超过半圆轨道的中点C，
则有： MvB2≤MgL
由能量关系有：EP= MvB2+4μMgL
解得： 
m≤M≤ 
m
【解析】（1）先研究弹簧竖直的情况，根据系统的机械能守恒求出弹簧最大的弹性势能；（2）弹簧如图放置时，由于弹簧的压缩量等于竖直放置时的压缩量，两种情况弹簧的弹性势能相等．由能量守恒定律求出物体P滑到B点时的速度，由机械能守恒定律求出物体P到达D点的速度．物体P离开D点后做平抛运动，由平抛运动的规律求水平距离；（3）根据能量守恒定律列式和临界条件求解．
【考点精析】本题主要考查了机械能守恒及其条件的相关知识点，需要掌握在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变才能正确解答此题．
