Question

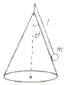
【题目】如图所示，半径为R的圆轮在竖直面内绕O轴匀速转动，轮上A、B两点均粘有一小物体，当B点转至最低位置时，此时O、A、B、P四点在同一竖直线上，已知：OA=AB，P是地面上的一点．A、B两点处的小物体同时脱落，最终落到水平地面上同一点．（不计空气的阻力）则OP的距离是（　　）

A. 7R

B. R

C. R

D. 5R

Answer 1

【答案】B

【解析】

首先分别求出AB两物体所圆轮圆周运动的线速度，即为做平抛的初速度；设出OP之间的距离，对AB两物体分别在水平方向和竖直方向上由运动学公式进行列式，即可解得OP之间的距离。

设OP之间的距离为h，则A下落的高度为h-，A随圆轮运动的线速度为，设A下落的时间为t1，水平位移为s，则在竖直方向上有：h-=g，在水平方向上有：s=t1，B下落的高度为h-R，B随圆轮运动的线速度为ωR，设B下落的时间为t2，水平位移也为s，在竖直方向上有：h-R=g，在水平方向上有：s=ωRt2，联立解得：h=R，故B正确，ACD错误。