题目内容
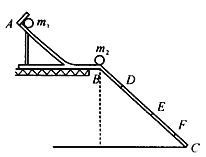
【题目】如图所示,传送带A、B间距离L=5 m且在同一水平面内,两个轮子半径均为r=0.2 m,半径R=0.4 m的固定竖直光滑圆轨道与传送带相切于B点,C点是圆轨道的最高点.当传送带静止不动时,质量m=1 kg的小煤块在A点以初速度v0=2![]() m/s开始运动,刚好能运动到C点.重力加速度g=10 m/s2.求:
m/s开始运动,刚好能运动到C点.重力加速度g=10 m/s2.求:
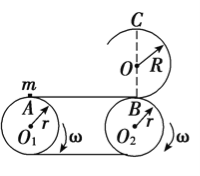
(1)当传送带的轮子以ω=10 rad/s的角速度匀速转动时,将小煤块无初速地放到传送带上的A点,求小煤块从A点运动到B点的过程中在传送带上划过痕迹的长度?
(2)当传送带的轮子匀速转动的角速度在什么范围内时,将小煤块无初速地放到传送带上的A点,小煤块运动到C点时对圆轨道的压力最大,最大压力FC是多大?
【答案】(1)0.5 m;(2)![]() ;50N
;50N
【解析】
试题分析:(1)当传送带静止不动时,小煤块刚好能运动到C点,则在C点,根据牛顿第二定律得:
![]() ①
①
小煤块从A→C过程中,由动能定理得:-μmgL-2mgR=![]() mv-
mv-![]() mv ②
mv ②
联立①②得μ=0.4
当传送带的轮子以ω=10 rad/s的角速度匀速转动时,传送带的线速度v=ωr=2 m/s
由![]() <L,得小煤块在传送带上加速的时间
<L,得小煤块在传送带上加速的时间![]()
小煤块与传送带的相对位移为l=vt-![]() t=0.5 m,即划过痕迹的长度为0.5 m
t=0.5 m,即划过痕迹的长度为0.5 m
(2)当小煤块在传送带上一直加速时,小煤块到达B点的速度最大,在C点对圆轨道的压力最大.设小煤块到达B点的最大速度为vB,则:μmgL=![]() mv解得vB=
mv解得vB=![]() m/s
m/s
传送带的线速度v≥![]() m/s,即传送带的角速度ω≥
m/s,即传送带的角速度ω≥![]() rad/s时,小煤块在C点对圆轨道的压力最大,小煤块从B→C,由机械能守恒定律得:2mgR=
rad/s时,小煤块在C点对圆轨道的压力最大,小煤块从B→C,由机械能守恒定律得:2mgR=![]() mv-
mv-![]() mv ③
mv ③
小煤块此时在C点,由牛顿第二定律得:![]() ④
④
联立③④得Fmax=50 N
根据牛顿第三定律得,对圆轨道最大压力FC=Fmax=50 N