题目内容
如图所示,质量m=0.2kg的小物体,从光滑曲面上高度H=0.8m处释放,到达底端时水平进入轴心距离L=6m的水平传送带,传送带可由一电机驱使逆时针转动。已知物体与传送带间的动摩擦因数 (取g=10m/s2)。
(取g=10m/s2)。
(1)求物体到达曲面底端时的速度大小?
(2)若电机不开启,传送带不转动,则物体滑离传送带右端的速度大小和在传送带上所用时间分别为多少?
(3)若开启电机,传送带以速率5m/s逆时针转动,则物体在传送带上滑动的过程中产生多少热量?
(1)4m/s(2) (3)3.2J
(3)3.2J
解析试题分析:(1)物体从曲面上下滑时机械能守恒,有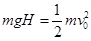
解得物体滑到底端时的速度 (2分)
(2分)
(2)设水平向右为正方向,物体滑上传送带后向右做匀减速运动,期间物体的加速度大小和方向都不变,加速度为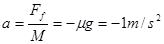 (1分)
(1分)
物体滑离传送带右端时速度为v1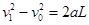
 (1分)
(1分)
由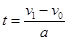 得,
得, (2分)
(2分)
(3)以地面为参考系,则滑上逆时针转动的传送带后,物体向右做匀减速运动.由以上计算可知,期间物体的加速度大小和方向都不变,所以到达右端时速度大小为2m/s,所用时间为2s,最后将从右端滑离传送带。此段时间内,
物体向右运动位移大小显然为6m
皮带向左运动的位移大小为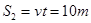
物体相对于传送带滑行的距离为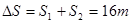 (2分)
(2分)
物体与传送带相对滑动期间产生的热量为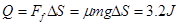 (2分)
(2分)
考点:机械能守恒定律;匀变速直线运动的速度与位移的关系;牛顿第二定律.
点评:传送带类题目要注意分析产生的热量即为摩擦力与相对位移间的乘积,再由能量守恒即可求得总能量,要注意分析能量间的相互转化.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目



