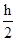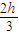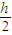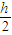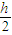题目内容
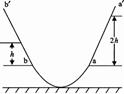
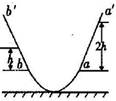
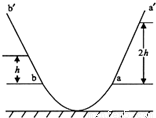
一光滑圆弧形的槽,槽底放在水平地面上,槽的两侧与坡度及粗细程度相同的两个斜坡aa’、bb’相切,相切处a、b位于同一水平面内,槽与斜坡在竖直平面内的截面如图所示.一小物块从斜坡aa’上距水平面ab的高度为2h处由静止沿斜坡滑下,并自a处进人槽内,到达b后沿斜坡bb’向上滑行,不考虑空气阻力,到达的最高处距水平面ab 的高度为h;接着小物块沿斜坡bb’滑下并从b处进人槽内反向运动,沿斜坡aa’向上滑行到达的最高处距水平面ab 的高度为 ( )

A. 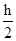 B.大于
B.大于
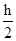
C.小于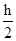 D.无法计算
D.无法计算
【答案】
A
【解析】
试题分析:设斜面与水平面的夹角是A,摩擦力大小为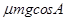 ,在第一个过程中,根据能量守恒,摩擦力做的负功等于重力做的正功
,在第一个过程中,根据能量守恒,摩擦力做的负功等于重力做的正功
重力做功为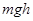 ,摩擦力做功的距离为
,摩擦力做功的距离为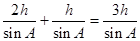 ,摩擦力做功为
,摩擦力做功为
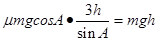 ,得出
,得出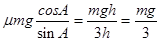
设第二次滑到距水平面x高处,同样的道理,有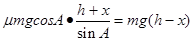
将前面的结果带入,得到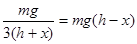 所以x=h/2,A正确,
所以x=h/2,A正确,
考点:考查了能量守恒的应用
点评:摩擦力做功和路径有关,在计算的时候需要注意

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 (2012?桂林模拟)一光滑圆弧形的槽,槽底放在水平地面上,槽的两侧与坡度及粗细程度相同的两个斜坡aa′、bb′相切,相切处a、b位于同一水平面内,槽与斜坡在竖直平面内的截面如图所示.一小物块从斜坡aa′上距水平面ab的高度为2h处由静止沿斜坡滑下,并自a处进人槽内,到达b后沿斜坡bb′向上滑行,不考虑空气阻力,到达的最高处距水平面ab 的高度为h;接着小物块沿斜坡bb′滑下并从b处进人槽内反向运动,沿斜坡aa′向上滑行到达的最高处距水平面ab 的高度为( )
(2012?桂林模拟)一光滑圆弧形的槽,槽底放在水平地面上,槽的两侧与坡度及粗细程度相同的两个斜坡aa′、bb′相切,相切处a、b位于同一水平面内,槽与斜坡在竖直平面内的截面如图所示.一小物块从斜坡aa′上距水平面ab的高度为2h处由静止沿斜坡滑下,并自a处进人槽内,到达b后沿斜坡bb′向上滑行,不考虑空气阻力,到达的最高处距水平面ab 的高度为h;接着小物块沿斜坡bb′滑下并从b处进人槽内反向运动,沿斜坡aa′向上滑行到达的最高处距水平面ab 的高度为( )