题目内容
16.某双星系统由两个质量分别为m1和m2的恒星组成,它们在相互引力的作用下,绕其连线上的某一点做周期相同的匀速圆周运动,已知两恒星之间的距离为L,万有引力常量为G,试求恒星m1的轨道半径和线速度大小.分析 两颗恒星都做匀速圆周运动,两颗恒星之间的万有引力提供向心力,根据牛顿第二定律列式求解两星体绕共同圆心做匀速圆周运动的轨道半径之比,结合两星体中心距离为L,求解出半径,然后进一步根据万有引力定律提供向心力列式求出线速度.
解答 解:两颗恒星都做匀速圆周运动,两颗恒星之间的万有引力提供向心力,根据牛顿第二定律,有:
对m1:$G\frac{{m}_{1}{m}_{2}}{{L}^{2}}={m}_{1}\frac{4{π}^{2}{r}_{1}}{{T}^{2}}$①
对m2:$G\frac{{m}_{1}{m}_{2}}{{L}^{2}}={m}_{2}\frac{4{π}^{2}{r}_{2}}{{T}^{2}}$②
故:m1r1=m2r2
由于r1+r2=L,解得:
r1=$\frac{{m}_{2}L}{{m}_{1}+{m}_{2}}$④
对于m1有$G\frac{{m}_{1}{m}_{2}}{{L}^{2}}={m}_{1}\frac{{{v}_{1}}^{2}}{{r}_{1}}$
解得:${v}_{1}={m}_{2}\sqrt{\frac{G}{({m}_{1}+{m}_{2})L}}$
答:恒星m1的轨道半径为$\frac{{m}_{2}L}{{m}_{1}+{m}_{2}}$,线速度大小为${m}_{2}\sqrt{\frac{G}{({m}_{1}+{m}_{2})L}}$.
点评 本题是双星问题,与卫星绕地球运动模型不同,两颗星都绕同一圆心做匀速圆周运动,关键抓住条件:角速度和周期相同.

练习册系列答案
相关题目
4.电磁波已广泛应用于很多领域.光波也是一种电磁波,下列说法正确的是( )
| A. | 手机发射和接收信号都是利用微波传送的 | |
| B. | 手机上网和WiFi上网都是利用光线传输信息的 | |
| C. | 常用的遥控器通过发射紫外线脉冲信号来遥控电视机 | |
| D. | 微波、红外线、紫外线、伦琴射线的频率依次减小 |
5.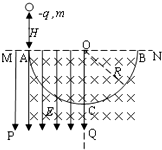 如图所示,ACB为光滑固定的半圆轨道,轨道半径为R,A,B为圆水平直径的两个端点,AC为$\frac{1}{4}$圆弧,MPQO为有界的竖直向下的匀强电场,电场强度的大小E=$\frac{2mg}{q}$,一个质量为m,电荷量为-q的带电小球.从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,已知重力加速度为g,关于带电小球的运动情况,下列说法正确的是( )
如图所示,ACB为光滑固定的半圆轨道,轨道半径为R,A,B为圆水平直径的两个端点,AC为$\frac{1}{4}$圆弧,MPQO为有界的竖直向下的匀强电场,电场强度的大小E=$\frac{2mg}{q}$,一个质量为m,电荷量为-q的带电小球.从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,已知重力加速度为g,关于带电小球的运动情况,下列说法正确的是( )
 如图所示,ACB为光滑固定的半圆轨道,轨道半径为R,A,B为圆水平直径的两个端点,AC为$\frac{1}{4}$圆弧,MPQO为有界的竖直向下的匀强电场,电场强度的大小E=$\frac{2mg}{q}$,一个质量为m,电荷量为-q的带电小球.从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,已知重力加速度为g,关于带电小球的运动情况,下列说法正确的是( )
如图所示,ACB为光滑固定的半圆轨道,轨道半径为R,A,B为圆水平直径的两个端点,AC为$\frac{1}{4}$圆弧,MPQO为有界的竖直向下的匀强电场,电场强度的大小E=$\frac{2mg}{q}$,一个质量为m,电荷量为-q的带电小球.从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,已知重力加速度为g,关于带电小球的运动情况,下列说法正确的是( )| A. | 若H=R,则小球到达C点的速度为零 | |
| B. | 若H=2R,则小球到达B点的速度为零 | |
| C. | 若H=3R,则小球到达C点的速度为$\sqrt{2gR}$ | |
| D. | 若H=4R,则小球到达b点的速度为$\sqrt{2gR}$ |
4.太阳系中一颗比地球小的行星,它运行轨道的长轴跟地球运行轨道的长轴之比约为16,则它绕太阳公转的周期约为( )
| A. | 8年 | B. | 64年 | C. | 200年 | D. | 16年 |
11.已知某行星表面的重力加速度为g,行星的半径为R,万有引力常量为G,不计行星自转,则( )
| A. | 该行星的质量为$\frac{g{R}^{2}}{G}$ | B. | 该行星的质量为$\frac{{g}^{2}R}{G}$ | ||
| C. | 该行星的平均密度为$\frac{3g}{4πGR}$ | D. | 该行星的平均密度为$\frac{3g}{4πG{R}^{2}}$ |
1.下列说法正确的是( )
| A. | 温度是分子平均动能的标志 | |
| B. | 做功和热传递是改变物体内能的两种方法 | |
| C. | 不可能使热量从低温物体传向高温物体 | |
| D. | 机械能可以全部转化为内能,内能也可能全部转化为机械能 |
8.小船以一定的速率垂直河岸向对岸划去,它渡河的时间、发生的位移与水速的关系正确的是( )
| A. | 水速小时,位移小,时间也小 | B. | 水速大时,位移大,时间也大 | ||
| C. | 水速大时,位移大,但时间不变 | D. | 位移与水速大小无关 |
5.关于重力做功、重力势能变化的说法正确的是( )
| A. | 当物体向下运动时,重力对物体做负功,重力势能减小 | |
| B. | 当物体向下运动时,重力对物体做正功,重力势能增大 | |
| C. | 当物体向上运动时,重力对物体做负功,重力势能增大 | |
| D. | 当物体向上运动时,重力对物体做正功,重力势能减小 |