题目内容
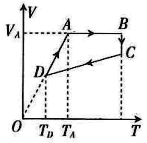
【题目】两电阻不计的光滑金属导轨固定在竖直平面内,导轨足够长且间距为l。两质量均为m、电阻均为R的导体棒M、N位于边界水平的匀强磁场上方,距磁场的上边界有一定高度,磁场竖直方向宽度为导体距水平边界高度的3倍,磁场大小为B,方向垂直导轨所在平面,如图所示。先由静止释放导体棒M,M进入磁场恰好匀速运动,此时再由静止释放导体棒N,两导体棒始终水平且与导轨保持良好接触。重力加速度取g,则下列说法正确的是( )

A.释放前导体棒M、N距磁场上边界的高度为![]()
B.导体棒M离开磁场时的速度![]()
C.导体棒M、N均进入磁场后,两棒间距离减小
D.两导体棒各自离开磁场时导体棒N的速度较小
【答案】BD
【解析】
A.设导体棒到磁场上边界的距离为h,导体棒刚进入磁场时的速度大小为v,根据动能定理有
![]()
得![]() ,导体棒M进入磁场后产生的感应电动势为
,导体棒M进入磁场后产生的感应电动势为
![]()
回路中的电流大小为
![]()
由于导体棒M做匀速直线运动,可知其所受合力为零,根据平衡条件有
![]()
联立可得![]() ,故A错误;
,故A错误;
B.结合前面的分析及题意可知,导体棒N刚进入磁场时的速度大小也为v,设导体棒N从开始到进入磁场所需要的时间为t,受力分析可知导体棒N在进入磁场之前做自由落体运动,由运动规律有
![]()
则可得此过程中导体棒M向下运动的位移为
![]()
因为磁场竖直方向宽度为导体距水平边界高度的3倍,则可知此时导体棒M到磁场的下边界距离为h,导体棒N进入磁场后,两棒的速度相同,而两棒都只受重力作用,加速度均为g,从此时开始两棒做加速度与初速度均相同的匀加速直线运动,则可知在导体棒M离开磁场之前,两棒的速度一直相同,所以回路中不产生感应电流,设导体棒M离开磁场时的速度大小为![]() ,由速度位移关系有
,由速度位移关系有
![]()
解得![]() ,故B正确;
,故B正确;
C.由B选项的分析可知,导体棒M、N均进入磁场后,两棒间距离保持不变,故C错误;
D.由前面的分析可知,导体棒M刚离开磁场时,导体棒N的速度大小也为![]() ,则可知此时导体棒N产生的感应电动势大于前面导体棒M单独切割时感应电动势,所以此时导体棒N所受安培力要比重力更大,根据楞次定律可知导体棒N所受安培力一定竖直向上,所以导体棒N所受合力向上,导体棒N做减速运动,则可知导体棒N离开磁场时的速度要小于导体棒M离开磁场的速度
,则可知此时导体棒N产生的感应电动势大于前面导体棒M单独切割时感应电动势,所以此时导体棒N所受安培力要比重力更大,根据楞次定律可知导体棒N所受安培力一定竖直向上,所以导体棒N所受合力向上,导体棒N做减速运动,则可知导体棒N离开磁场时的速度要小于导体棒M离开磁场的速度![]() ,故D正确。
,故D正确。
故选BD。

【题目】在“测量蓄电池的电动势和内阻”实验中:
(1)小明按图甲所示的电路图进行实验操作,调整滑动变阻器测得5组电流和电压的数据,如表中所示。
电流I/A | 1.72 | 1.35 | 0.98 | 0.63 | 0.34 |
电压U/V | 1.88 | 1.92 | 1.93 | 1.97 | 1.99 |
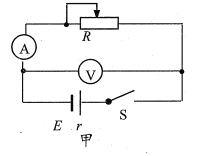
①请在图乙中作出蓄电池路端电压U随电流I变化的U一I图象______;
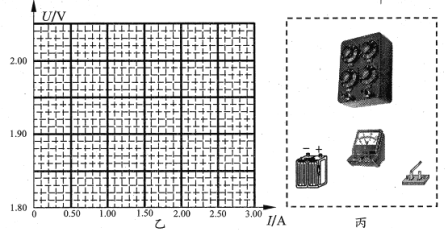
②根据U—I图象得到蓄电池电动势E=________V,内阻r=________Ω。
(2)实验时,小明进行了多次测量,耗费了较长时间,测量期间一直保持电路闭合。其实,从实验误差考虑,这样的操作不妥,因为_________。
(3)小明再次实验时发现电流表坏了,于是移去电流表,同时用电阻箱替换滑动变阻器。重新连接实验电路,仍然通过U一I图象处理实验数据,测得电动势和内阻的值。
①请在图丙虚线框中连接出相应的电路___________;
②简要说明得到U一I图象中电流I数据的方法__________。