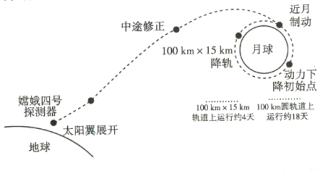
ЬтФПФкШн
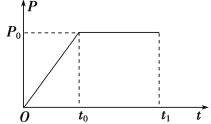
ЁОЬтФПЁПгУвЛИљЩўзгЪњжБЯђЩЯРвЛИіЮяПщЃЌЮяПщДгОВжЙПЊЪМдЫЖЏЃЌЩўзгРСІЕФЙІТЪАДШчЭМЫљЪОЙцТЩБфЛЏЃЌ0ЁЋt0ЪБМфФкЮяПщзідШМгЫйжБЯпдЫЖЏЃЌt0ЪБПЬКѓЮяЬхМЬајМгЫйЃЌt1ЪБПЬЮяПщДяЕНзюДѓЫйЖШЃЎвбжЊЮяПщЕФжЪСПЮЊmЃЌжиСІМгЫйЖШЮЊgЃЌдђЯТСаЫЕЗЈе§ШЗЕФЪЧ(ЁЁЁЁ)
A. ЮяПщЪМжезідШМгЫйжБЯпдЫЖЏ
B. 0ЁЋt0ЪБМфФкЮяПщЕФМгЫйЖШДѓаЁЮЊ![]()
C. t0ЪБПЬЮяПщЕФЫйЖШДѓаЁЮЊ![]()
D. 0ЁЋt1ЪБМфФкЩўзгРСІзіЕФзмЙІЮЊ![]()
ЁОД№АИЁПD
ЁОНтЮіЁП
гЩЭМПЩжЊдк0-t0ЪБМфФкЮяПщзідШМгЫйжБЯпдЫЖЏЃЌt0ЪБПЬКѓЙІТЪБЃГжВЛБфЃЌИљОнP=FvжЊЃЌvдіДѓЃЌFМѕаЁЃЌЮяПщзіМгЫйЖШМѕаЁЕФМгЫйдЫЖЏЃЌЕБМгЫйЖШМѕаЁЕНСуЃЌЮяЬхзідШЫйжБЯпдЫЖЏЃЌЙЪAДэЮѓЃЛИљОнP0=Fv=FatЃЌгЩХЃЖйЕкЖўЖЈТЩЕУЃКF=mg+maЃЌСЊСЂПЩЕУЃКP=ЃЈmg+maЃЉatЃЌгЩДЫПЩжЊЭМЯпЕФаБТЪЮЊЃК![]() ЃЌПЩжЊ
ЃЌПЩжЊ![]() ЃЌЙЪBДэЮѓЃЛдкt1ЪБПЬЫйЖШДяЕНзюДѓЃЌF=mgЃЌдђЫйЖШЃК
ЃЌЙЪBДэЮѓЃЛдкt1ЪБПЬЫйЖШДяЕНзюДѓЃЌF=mgЃЌдђЫйЖШЃК![]() ЃЌПЩжЊt0ЪБПЬЮяПщЕФЫйЖШДѓаЁаЁгк
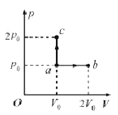
ЃЌПЩжЊt0ЪБПЬЮяПщЕФЫйЖШДѓаЁаЁгк![]() ЃЌЙЪCДэЮѓЃЛдкP-tЭМЯѓжаЃЌЭМЯпЮЇГЩЕФУцЛ§БэЪОЧЃв§СІзіЙІЕФДѓаЁМДЃК
ЃЌЙЪCДэЮѓЃЛдкP-tЭМЯѓжаЃЌЭМЯпЮЇГЩЕФУцЛ§БэЪОЧЃв§СІзіЙІЕФДѓаЁМДЃК![]() ЃЌЙЪDе§ШЗЁЃЫљвдDе§ШЗЃЌABCДэЮѓЁЃ
ЃЌЙЪDе§ШЗЁЃЫљвдDе§ШЗЃЌABCДэЮѓЁЃ

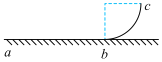
ЁОЬтФПЁПШчЭМЫљЪОЃЌзуЙЛГЄЕФЙтЛЌЦНааЕМЙьMNЁЂPQЧуаБЗХжУЃЌСНЕМЙьМфОрРыЮЊ![]() ЃЌЕМЙьЦНУцгыЫЎЦНУцМфЕФМаНЧЮЊ
ЃЌЕМЙьЦНУцгыЫЎЦНУцМфЕФМаНЧЮЊ![]() ЃЌДХИагІЧПЖШЮЊBЕФдШЧПДХГЁДЙжБгкЕМЙьЦНУцЯђЩЯЃЌЕМЙьЕФMЁЂPСНЖЫСЌНгзшжЕЮЊ
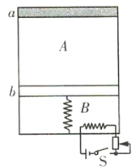
ЃЌДХИагІЧПЖШЮЊBЕФдШЧПДХГЁДЙжБгкЕМЙьЦНУцЯђЩЯЃЌЕМЙьЕФMЁЂPСНЖЫСЌНгзшжЕЮЊ![]() ЕФЕчзшЃЌН№ЪєАєabДЙжБгкЕМЙьЗХжУВЂгУЯИЯпЭЈЙ§ЙтЛЌЖЈЛЌТжгыжиЮяЯрСЌЃЌН№ЪєАєabЕФжЪСП
ЕФЕчзшЃЌН№ЪєАєabДЙжБгкЕМЙьЗХжУВЂгУЯИЯпЭЈЙ§ЙтЛЌЖЈЛЌТжгыжиЮяЯрСЌЃЌН№ЪєАєabЕФжЪСП![]() ЃЌЕчзш
ЃЌЕчзш![]() ЃЌжиЮяЕФжЪСП
ЃЌжиЮяЕФжЪСП![]() ЃЌШчЙћНЋН№ЪєАєКЭжиЮягЩОВжЙЪЭЗХЃЌН№ЪєАєбиаБУцЩЯЛЌЕФОрРыгыЪБМфЕФЙиЯЕШчБэЫљЪОЃЌВЛМЦЕМЙьЕчзшЃЌgШЁ
ЃЌШчЙћНЋН№ЪєАєКЭжиЮягЩОВжЙЪЭЗХЃЌН№ЪєАєбиаБУцЩЯЛЌЕФОрРыгыЪБМфЕФЙиЯЕШчБэЫљЪОЃЌВЛМЦЕМЙьЕчзшЃЌgШЁ![]() ЧѓЃК
ЧѓЃК
ЪБМфtЃЈsЃЉ | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
ЩЯЛЌОрРыЃЈmЃЉ | 0 | 0.05 | 0.15 | 0.35 | 0.70 | 1.05 | 1.40 |
(1)abАєзюжезідШЫйжБЯпдЫЖЏЕФЫйЖШЪЧЖрЩйЃП
(2)ДХИагІЧПЖШBЕФДѓаЁЪЧЖрЩйЃП
(3)ЕБН№ЪєАєabЕФЫйЖШ![]() ЪБЃЌН№ЪєАєabЩЯЛЌЕФМгЫйЖШДѓаЁЪЧЖрЩйЃП
ЪБЃЌН№ЪєАєabЩЯЛЌЕФМгЫйЖШДѓаЁЪЧЖрЩйЃП