题目内容
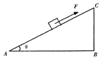
 如图所示,有一个重量为20N的小物体放在斜面上,斜面底边长AB=40cm,高BC=30cm,物体与斜面之间的动摩擦因数为μ=0.5,物体在一沿斜面向上的大小为F=20N的力作用下处于静止状态,现将力F顺时针转动至水平向右,则此时的摩擦力大小为( )
如图所示,有一个重量为20N的小物体放在斜面上,斜面底边长AB=40cm,高BC=30cm,物体与斜面之间的动摩擦因数为μ=0.5,物体在一沿斜面向上的大小为F=20N的力作用下处于静止状态,现将力F顺时针转动至水平向右,则此时的摩擦力大小为( )分析:对物体受力分析,受重力、支持力、推力、静摩擦力,根据平衡条件列式求解.
解答:解:当力F沿斜面向上时,F=mgsinθ+μmgcosθ 由sin2θ+cos2θ=1 得:sinθ=0.6 cosθ=0.8
对物体受力分析,受重力、支持力、推力、静摩擦力,如图所示;
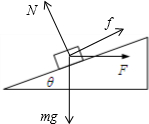
将重力和推力F沿着平行斜面和垂直斜面方向正交分解,根据平衡条件,有:
平行斜面方向:Fcosθ+f-mgsinθ=0;
垂直斜面方向:N-mgcosθ-Fsinθ=0;
联立解得:N=mgcosθ+Fsinθ;
f=mgsinθ-Fcosθ=20×0.6-20×0.8=-4N,负号代表方向沿斜面向下.
故选:D.
对物体受力分析,受重力、支持力、推力、静摩擦力,如图所示;

将重力和推力F沿着平行斜面和垂直斜面方向正交分解,根据平衡条件,有:
平行斜面方向:Fcosθ+f-mgsinθ=0;
垂直斜面方向:N-mgcosθ-Fsinθ=0;
联立解得:N=mgcosθ+Fsinθ;
f=mgsinθ-Fcosθ=20×0.6-20×0.8=-4N,负号代表方向沿斜面向下.
故选:D.
点评:本题考查了受力平衡以及正交分解的应用,本题关键是结合数学知识将sinθ确定出来.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
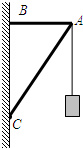 如图所示,有一个固定在竖直墙壁上的三角支架ABC,AB杆沿水平方向,AC杆与AB杆的夹角为60°,当在A点悬挂一物体时,AB杆受到的拉力为10N,求 AC杆受的压力及悬挂物体的重量.
如图所示,有一个固定在竖直墙壁上的三角支架ABC,AB杆沿水平方向,AC杆与AB杆的夹角为60°,当在A点悬挂一物体时,AB杆受到的拉力为10N,求 AC杆受的压力及悬挂物体的重量. 如图所示,有一个固定在竖直墙壁上的三角支架ABC,AB杆沿水平方向,AC杆与AB杆的夹角为60°,当在A点悬挂一物体时,AB杆受到的拉力为10N,求 AC杆受的压力及悬挂物体的重量.
如图所示,有一个固定在竖直墙壁上的三角支架ABC,AB杆沿水平方向,AC杆与AB杆的夹角为60°,当在A点悬挂一物体时,AB杆受到的拉力为10N,求 AC杆受的压力及悬挂物体的重量.