题目内容
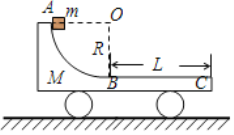
【题目】如图，质量为M的小车静止在光滑的水平面上，小车AB段是半径为R的四分之一光滑圜弧轨道，BC段是长为L的水平粗糙轨道，两段轨道相切于B点，一质量为m的滑块在小车上从A点由静止开始沿轨道滑下，然后滑入BC轨道，最后恰好停在C点。已知小车质量M=2m，滑块与轨道BC间的动摩擦因数为μ，重力加速度为g。则滑块从A运动到C的过程中
A. 滑块水平方向相对地面的位移大小为
B. 小车相对地面的位移大小为
C. 小车M的最大速度
D. 滑块克服摩擦力做的功在数值上等于滑块减少的机械能
【答案】AC
【解析】
A、B、设全程小车相对地面的位移大小为s，滑块水平方向相对地面的位移为x，滑块与小车组成的系统在水平方向动量守恒且满足人船模型：x+s =R+L， 
，已知M=2m，解得：
，
，故A正确，B错误.
C、滑块刚滑到B点时小车受到滑块的压力一直做正功，小车的速度达到最大，取水平向右为正方向，由动量守恒定律和机械能守恒分别得
，
，解得
；故C正确.
D、滑块从B点开始和车相对滑动，滑动摩擦力对滑块做负功，根据动能定理知滑块克服摩擦力做的功等于滑块减少的动能；全过程滑块减少的机械能转化为系统生热；D错误.
故选AC.
练习册系列答案
阅读快车系列答案
相关题目
