题目内容
某天文台测得某行星的一颗卫星绕行星做匀速圆周运动,测得其轨道半径为R,周期为T,则其向心加速度为 ;行星的质量为 .(已知万有引力恒量为G)
分析:已知周期,即可知道角速度的大小,根据a=Rω2求出向心加速度的大小.根据万有引力提供向心力求出行星的质量.
解答:解:卫星的向心加速度a=Rω2=(
) 2R.
根据G
=mR(
)2得,M=
.
故答案为:(
) 2R,
.
| 2π |
| T |
根据G
| Mm |
| R2 |
| 2π |
| T |
| 4π2R3 |
| GT2 |
故答案为:(
| 2π |
| T |
| 4π2R3 |
| GT2 |
点评:解决本题的关键掌握向心加速度与轨道半径和周期的关系,以及掌握万有引力提供向心力这一理论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2011?静安区二模)(A)某天文台测得某行星的一颗卫星绕行星做匀速圆周运动,测得其轨道半径为R,周期为T,则其向心加速度为
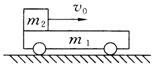
(2011?静安区二模)(A)某天文台测得某行星的一颗卫星绕行星做匀速圆周运动,测得其轨道半径为R,周期为T,则其向心加速度为 =0.5,则小车的最大速度是____ m/s;物块在车面上滑行的时间是_____ s。
=0.5,则小车的最大速度是____ m/s;物块在车面上滑行的时间是_____ s。