题目内容
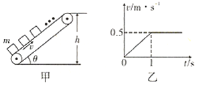
【题目】如图甲所示，工厂利用倾角θ=37°的皮带传输机，将每个质量m= 8kg的木箱从地面运送到高h=3.15m的平台上，机械手每隔1s就将一个木箱放到传送带的底端，传送带的皮带以恒定的速度顺时针转动且不打滑。木箱放到传送带上的部分v-t图象如图乙所示，已知各木箱与传送带间的动摩擦因数都相等。若最大静摩擦力等于滑动摩擦力，g取10m/s2。求：
(1)木箱与传送带间的动摩擦因数μ；
(2)传送带上最多有几个木箱同时在向上输送；
(3)皮带传输机由电动机带动，从机械手放上第一个木箱开始计时的1分钟内，因为木箱的放人，电动机 需要多做的功（不考虑电动机能量损耗）
【答案】(1)
(2)11 (3)14640J
【解析】
(1)由乙图得出木箱运动的加速度和皮带运动的速度，根据牛顿第二定律求解动摩擦因数μ；
(2)根据运动学基本公式求出木箱加速的位移，木箱相对皮带静止后，相邻两个木箱之间的距离都相等，结合传送带的长度列式求解即可；
(3)先求出一个木箱在传送带上运动时产生的热量和增加的动能和重力势能，再求出从开始的1分钟内共传送木箱的个数，求和即可电动机需要多做的功.
(1)由乙图可知，木箱运动的加速度为：
皮带匀速运动的速度为：v=0.5m/s，
根据牛顿第二定律得：μmgcosθ-mgsinθ=ma
解得：
(2)木箱加速运动的位移为：
木箱相对皮带静止后，相邻两个木箱之间的距离都相等，有：△L=vt=0.5m
传送带的长度为： 
L=10△L+x1
所以传送带上最多同时存在的木箱个数为11个
(3)木箱再传送带上运动时，和皮带间的相对位移为：△x=vt-x1=0.5×1-0.25=0.25m，
和皮带间的摩擦产生的热量为：Q1=μmgcosθ△x=13J
木箱最终增加的动能为：
木箱到达平台增加的重力势能为：EP1=mgh=252J
从开始的1分钟内共传送木箱的个数N=1×60=60个，其中50个已经到达平台，还有10个正在传送带上，
到达平台的50个，电动机做的功为：W1=50（Q1+EK1+EP1）=13300J，
在传送带上的已经开始运动得10个木箱增加的动能为：10EK1=10J，
10个木箱的摩擦生热为：10Q1=130J，
10个木箱增加的重力势能共为：EP′=10mg△xsin37°+mg△Lsin37°+2mg△Lsin37°+…+9mg△Lsin37°=10mg△xsin37°+mg△Lsin37°（1+2+3+…+9）=1200J，
所以电动机多做的功为：W=W1+10EK1+10Q1+EP′=14640J
