题目内容
有一段长为L，与水平面夹角为θ的斜坡路面，一质量为m的木箱放在斜坡底端，一质量为M的人想沿斜坡将木箱推上坡顶，假设木箱与路面间的摩擦因数与人与地面之间的动摩擦因数均为μ，人是沿与斜坡平行的方向用力推木箱的，求人将木箱由坡底推到坡顶所需的最短时间及到达坡顶时木箱获得的速度大小．（运算中可认为最大静摩擦力等于滑动摩擦力，重力加速度为g）
解：取人和木箱一体为研究对象
要使木箱从坡底到坡顶所用时间最短，须使人受静摩擦力最大
根据牛顿第二定律
μMgcosθ-μmgcosθ-（M+m）gsinθ=（M+m）a…（1）
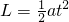…（2）
收（1）、（2）两式得：
由v2=2aL得，v=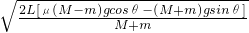
．
答：人将木箱由坡底推到坡顶所需的最短时间，到达坡顶时木箱获得的速度大小v=．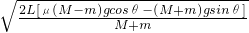
分析：根据牛顿第二定律求出人和木箱整体的加速度，结合位移时间公式和速度位移公式求出人将木箱由坡底推到坡顶所需的最短时间及到达坡顶时木箱获得的速度大小．
点评：本题考查了牛顿第二定律和运动学公式的综合运用，知道加速度是联系力学和运动学的桥梁．
要使木箱从坡底到坡顶所用时间最短，须使人受静摩擦力最大
根据牛顿第二定律
μMgcosθ-μmgcosθ-（M+m）gsinθ=（M+m）a…（1）
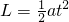…（2）收（1）、（2）两式得：
由v2=2aL得，v=
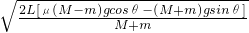．答：人将木箱由坡底推到坡顶所需的最短时间
，到达坡顶时木箱获得的速度大小v=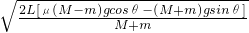．分析：根据牛顿第二定律求出人和木箱整体的加速度，结合位移时间公式和速度位移公式求出人将木箱由坡底推到坡顶所需的最短时间及到达坡顶时木箱获得的速度大小．
点评：本题考查了牛顿第二定律和运动学公式的综合运用，知道加速度是联系力学和运动学的桥梁．
练习册系列答案
阅读快车系列答案
相关题目
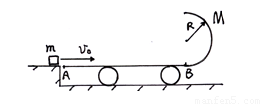
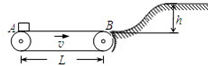为了节能，某货场设计了如图所示的送货装置，长为L的水平传送带右端B与一光滑弧面相连，弧面顶端为储货平台，将货物无初速度轻放在传送带左端A，通过传送带到达B端时具有一定动能，货物可以利用此动能滑上储货平台，平台离传送带高h，在安装调试时传送带以某一速度匀速运动，工人发现货物只能上滑到
如图所示，在光滑的水平面上有一段长为L、质量分布均匀的绳子，绳子在水平向左的恒力F作用下做匀加速直线运动．绳子上某一点到绳子右端的距离为x，设该处的张力为T，则能正确描述T与x之间的关系的图象是（ ）
光滑圆弧轨道，圆弧轨道与水平轨道在O′点相切。车右端固定一个尺寸和质量可以忽略、处于锁定状态的压缩弹簧，一质量为m的小物块紧靠弹簧放置，小物块与水平轨道间的动摩擦因数为μ，整个装置处于静止状态。现将弹簧解除锁定，小物块被弹出，恰能到达圆弧轨道的最高点A。将小物块视为质点，求：