题目内容
长度1m的轻绳下端挂着一质量为9.99kg的沙袋，一颗质量为10g的子弹以500m/s的速度水平射入沙袋（未穿出），求在子弹射入沙袋后的瞬间，悬绳的拉力是多大？（设子弹与沙袋的接触时间很短，g取10m/s2）
子弹射入沙袋的过程，对它们组成的系统，遵守动量守恒定律，取子弹射入前的速度方向为正方向，则得：
mv0=（M+m）v
解得：v=
=
m/s=0.5m/s
子弹射入沙袋后的瞬间，由重力和绳子的拉力的合力提供向心力，则由牛顿第二定律得：
F-(M+m)g=(M+m)
，
解得：F=(M+m)g+(M+m)
=(9.99+0.01)×10N+(9.99+0.01)
N=102.5N
答：在子弹射入沙袋后的瞬间，悬绳的拉力是102.5N．
mv0=（M+m）v
解得：v=
| mv0 |
| M+m |
| 0.01×500 |
| 9.99+0.01 |
子弹射入沙袋后的瞬间，由重力和绳子的拉力的合力提供向心力，则由牛顿第二定律得：
F-(M+m)g=(M+m)
| v2 |
| l |
解得：F=(M+m)g+(M+m)
| v2 |
| l |
| 0.52 |
| 1 |
答：在子弹射入沙袋后的瞬间，悬绳的拉力是102.5N．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
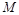的小车，车上表面水平且光滑，车上装有半径为
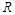的光滑四分之一圆环轨道，圆环轨道质量不计且与车的上表面相切，质量为
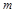的小滑块从跟车面等高的平台以
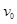的初速度滑上小车（
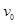足够大，以至滑块能够滑过与环心O等高的b点），试求：
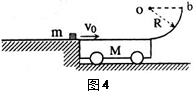（2）滑块从滑上小车至滑到环心O等高的b点过程中，车的上表面和环的弹力共对滑块做了多少功？
