题目内容
 (2010?南通二模)如图所示,有界匀强磁场磁感应强度为B,方向垂直纸面向里,MN为其左边界,磁场中放置一半径为R的圆柱形金属圆筒,圆心O到MN的距离OO1=2R,圆筒轴线与磁场平行.圆筒用导线通过一个电阻r0接地,最初金属圆筒不带电.现有范围足够大的平行电子束以速度v0从很远处沿垂直于左边界MN向右射入磁场区,已知电子质量为m,电量为e.
(2010?南通二模)如图所示,有界匀强磁场磁感应强度为B,方向垂直纸面向里,MN为其左边界,磁场中放置一半径为R的圆柱形金属圆筒,圆心O到MN的距离OO1=2R,圆筒轴线与磁场平行.圆筒用导线通过一个电阻r0接地,最初金属圆筒不带电.现有范围足够大的平行电子束以速度v0从很远处沿垂直于左边界MN向右射入磁场区,已知电子质量为m,电量为e.(1)若电子初速度满足v0=
| 3eBR | m |
(2)当圆筒上电量达到相对稳定时,测量得到通过电阻r0的电流恒为I,忽略运动电子间的相互作用,求此时金属圆筒的电势φ和电子到达圆筒时速度v(取无穷远处或大地电势为零).
(3)在(2)的情况下,求金属圆筒的发热功率.
分析:(1)由牛顿第二定律可求得粒子的转动半径,画出粒子的运动轨迹可得出几何关系,从而确定出到圆筒上的电子对应MN边界上O1两侧的范围;
(2)由欧姆定律可求得圆柱体与地面间的电势差,则可求得金属圆桶的电势;由动能定理可求得电子射到圆柱表面时的速度;
(3)由电流的微观定义可求得电子数,则可求得电子具有的总能量,由能量守恒可求得圆筒上的发热功率.
(2)由欧姆定律可求得圆柱体与地面间的电势差,则可求得金属圆桶的电势;由动能定理可求得电子射到圆柱表面时的速度;
(3)由电流的微观定义可求得电子数,则可求得电子具有的总能量,由能量守恒可求得圆筒上的发热功率.
解答: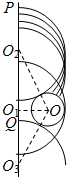 解:(1)如图所示,设电子进入磁场回旋轨道半径为r,则 qv0B=m
解:(1)如图所示,设电子进入磁场回旋轨道半径为r,则 qv0B=m
解得 r=3R
大量电子从MN上不同点进入磁场轨迹如图,从O1上方P点射入的电子刚好擦过圆筒O1O2=
=2
R
O1P=O1O2+r=(3+2
)R
同理可得到O1下Q点距离O1Q=(2
-3)R.
(2)稳定时,圆柱体上电荷不再增加,与地面电势差恒为U,
U=Ir0
电势 φ=-Ir0
电子从很远处射到圆柱表面时速度为v,有-eU=
mv2-
m
解得 v=
.
(3)电流为I,单位时间到达圆筒的电子数 n=
电子所具有总能量 E=n×
m
=
消耗在电阻上的功率 Pr=I2r0
所以圆筒发热功率 P=
-I2r0.
 解:(1)如图所示,设电子进入磁场回旋轨道半径为r,则 qv0B=m
解:(1)如图所示,设电子进入磁场回旋轨道半径为r,则 qv0B=m
| ||
| r |
大量电子从MN上不同点进入磁场轨迹如图,从O1上方P点射入的电子刚好擦过圆筒O1O2=
| (4R)2-(2R)2 |
| 3 |
O1P=O1O2+r=(3+2
| 3 |
同理可得到O1下Q点距离O1Q=(2
| 3 |
(2)稳定时,圆柱体上电荷不再增加,与地面电势差恒为U,
U=Ir0
电势 φ=-Ir0
电子从很远处射到圆柱表面时速度为v,有-eU=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
解得 v=
|
(3)电流为I,单位时间到达圆筒的电子数 n=
| I |
| e |
电子所具有总能量 E=n×
| 1 |
| 2 |
| v | 2 0 |
mI
| ||
| 2e |
消耗在电阻上的功率 Pr=I2r0
所以圆筒发热功率 P=
mI
| ||
| 2e |
点评:带电粒子在磁场中的运动解题时常常要根据题意做出可能的轨迹图,然后再根据几何关系即可确定出要求的问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2010?南通二模)如图所示,质量为M、长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间滑动摩擦力大小为f,用水平的恒定拉力F作用于滑块.当滑块运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
(2010?南通二模)如图所示,质量为M、长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间滑动摩擦力大小为f,用水平的恒定拉力F作用于滑块.当滑块运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )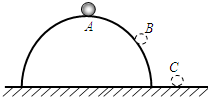 (2010?南通二模)竖直平面内光滑圆轨道外侧,一小球以某一水平速度v0从A点出发沿圆轨道运动,至B点时脱离轨道,最终落在水平面上的C点,不计空气阻力.下列说法中不正确的是( )
(2010?南通二模)竖直平面内光滑圆轨道外侧,一小球以某一水平速度v0从A点出发沿圆轨道运动,至B点时脱离轨道,最终落在水平面上的C点,不计空气阻力.下列说法中不正确的是( ) (2010?南通二模)如图所示,xOy坐标平面在竖直面内,x轴沿水平方向,y轴正方向竖直向上,在图示空间内有垂直于xOy平面的水平匀强磁场.一带电小球从O点由静止释放,运动轨迹如图中曲线.关于带电小球的运动,下列说法中正确的是( )
(2010?南通二模)如图所示,xOy坐标平面在竖直面内,x轴沿水平方向,y轴正方向竖直向上,在图示空间内有垂直于xOy平面的水平匀强磁场.一带电小球从O点由静止释放,运动轨迹如图中曲线.关于带电小球的运动,下列说法中正确的是( )