题目内容
【题目】竖直平面内有一圆形绝缘细管,细管截面半径远小于半径R,在中心处固定一带电荷量为+Q的点电荷.质量为m、带电荷量为+q的带电小球在圆形绝缘细管中做圆周运动,当小球运动到最高点时恰好对管无作用力,求当小球运动到最低点时对管壁的作用力.
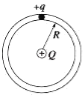
【答案】当小球运动到最低点时对管壁的作用力为6mg.
【解析】
试题分析:在最高点是重力和电场力的合力提供向心力,根据牛顿第二定律列式;在最低点,重力、电场力和支持力的合力提供向心力,根据牛顿第二定律列式;从最高点到最低点过程只有重力做功,根据动能定理列式;最后联立求解即可.
解:在最高点是重力提供向心力,故:
mg﹣F=m![]()
最低点,重力和支持力的合力提供向心力,故:
N﹣mg﹣F=m![]()
从最高点到最低点过程只有重力做功,根据动能定理,有:
mg2R=![]()
其中:
F=![]()
联立解得:
N=6mg
根据牛顿第三定律,压力为6mg;
答:当小球运动到最低点时对管壁的作用力为6mg.

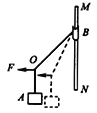
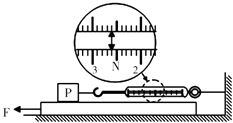
【题目】如图,把弹簧测力计的一端固定在墙上,用力F水平向左拉金属板,金属板向左运动,此时测力计的示数稳定(图中已把弹簧测力计的示数放大画出),则物块P与金属板间的滑动摩擦力的大小是 N.若用弹簧测力计测得物块P重10.40N,根据表中给出的动摩擦因数,可推算出物块P的材料为 .
材料 | 动摩擦因数 |
金属﹣金属 | 0.25 |
橡胶﹣金属 | 0.30 |
木头﹣金属 | 0.20 |
皮革﹣金属 | 0.28 |
【题目】某实验小组利用如图1所示的装置探究加速度与力、质量的关系.
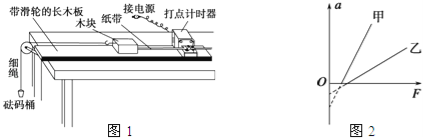
①下列做法正确的是 (填字母代号)
A.调节滑轮的高度,使牵引木块的细绳与长木板保持平行 |
B.在调节木板倾斜度平衡木块受到的滑动摩擦力时,将装有砝码的砝码桶通过定滑轮拴木块上 |
C.实验时,先放开木块再接通打点计时器的电源 |
D.通过增减木块上的砝码改变质量时,不需要重新调节木板倾斜度 |
②为使砝码桶及桶内砝码的总重力在数值上近似等于木块运动时受到的拉力,应满足的条件是砝码桶及桶内砝码的总质量 木块和木块上砝码的总质量(填远大于,远小于,或近似于)
③甲、乙两同学在同一实验室,各取一套图1的装置放在水平桌面上,木块上均不放砝码,在没有平衡摩擦力的情况下,研究加速度a与拉力F的关系,分别得到图2中甲、乙两条直线.设甲、乙用的木块质量分别为m甲,m乙.甲、乙用的木块与木板间的动摩擦因数分别为μ甲,μ乙,由图象可知,m甲 m乙;μ甲 μ乙(填“大于”、“小于”或“等于”)