题目内容
14.关于匀速圆周运动的物理量,说法正确的是( )| A. | 半径一定时,线速度与角速度成正比 | |
| B. | 周期一定时,线速度与角速度成正比 | |
| C. | 线速度一定时,角速度与半径成正比 | |
| D. | 角速度一定时,线速度与半径成反比 |
分析 根据线速度、角速度、周期和半径的关系公式v=ωr、$ω=\frac{2π}{T}$进行判断.
解答 解:A、根据公式v=ωr,只有当半径一定时,角速度与线速度成正比,故A正确;
B、周期一定时,由$ω=\frac{2π}{T}$则角速度一定,此时线速度与角速度成正比.故B正确;
C、根据公式v=ωr,线速度一定,角速度与半径成反比,故C错误;
D、根据公式v=ωr,角速度一定,线速度与半径成正比,故D错误;
故选:AB
点评 本题关键记住公式v=ωr,然后结合控制变量法进行分析,基础题.

练习册系列答案
相关题目
5. 如图所示,A为静止于地球赤道上的物体,B为绕地球做匀速圆周运动轨道半径为r的卫星,C为绕地球沿椭圆轨道运动的卫星,长轴大小为a,P为B、C两卫星轨道的交点,已知A、B、C绕地心运动的周期相同,下列说法正确的是( )
如图所示,A为静止于地球赤道上的物体,B为绕地球做匀速圆周运动轨道半径为r的卫星,C为绕地球沿椭圆轨道运动的卫星,长轴大小为a,P为B、C两卫星轨道的交点,已知A、B、C绕地心运动的周期相同,下列说法正确的是( )
 如图所示,A为静止于地球赤道上的物体,B为绕地球做匀速圆周运动轨道半径为r的卫星,C为绕地球沿椭圆轨道运动的卫星,长轴大小为a,P为B、C两卫星轨道的交点,已知A、B、C绕地心运动的周期相同,下列说法正确的是( )
如图所示,A为静止于地球赤道上的物体,B为绕地球做匀速圆周运动轨道半径为r的卫星,C为绕地球沿椭圆轨道运动的卫星,长轴大小为a,P为B、C两卫星轨道的交点,已知A、B、C绕地心运动的周期相同,下列说法正确的是( )| A. | 物体A的线速度大于卫星B的线速度 | |
| B. | 卫星B离地面的高度可以为任意值 | |
| C. | a与r长度关系满足a=2r | |
| D. | 若已知物体A的周期和万有引力常量,可求出地球的平均密度 |
2.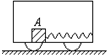 如图所示水平面上,质量为1kg的物块A拴在一个被水平拉伸的弹簧一端,弹簧的另一端固定在小车上,小车静止不动,弹簧对物块的弹力大小为0.3N时,物块处于静止状态,若小车以加速度a=0.5m/s2沿水平地面向右加速运动时( )
如图所示水平面上,质量为1kg的物块A拴在一个被水平拉伸的弹簧一端,弹簧的另一端固定在小车上,小车静止不动,弹簧对物块的弹力大小为0.3N时,物块处于静止状态,若小车以加速度a=0.5m/s2沿水平地面向右加速运动时( )
 如图所示水平面上,质量为1kg的物块A拴在一个被水平拉伸的弹簧一端,弹簧的另一端固定在小车上,小车静止不动,弹簧对物块的弹力大小为0.3N时,物块处于静止状态,若小车以加速度a=0.5m/s2沿水平地面向右加速运动时( )
如图所示水平面上,质量为1kg的物块A拴在一个被水平拉伸的弹簧一端,弹簧的另一端固定在小车上,小车静止不动,弹簧对物块的弹力大小为0.3N时,物块处于静止状态,若小车以加速度a=0.5m/s2沿水平地面向右加速运动时( )| A. | 物块A相对小车仍静止 | B. | 物块A受到的摩擦力将减小 | ||
| C. | 物块A受到的摩擦力大小不变 | D. | 物块A受到的弹力将增大 |
9.某人造地球卫星绕地球做匀速圆周运动,假如它的轨道半径增加到原来的n倍后,仍能够绕地球做匀速圆周运动,则( )
| A. | 根据v=ωr,可知卫星运动的线速度将增大到原来的n倍 | |
| B. | 根据F=$\frac{m{v}^{2}}{r}$,可知卫星受到的向心力将减小到原来的$\frac{1}{n}$倍 | |
| C. | 根据F=$\frac{GMm}{{r}^{2}}$,可知地球给卫星提供的向心力将减小到原来的$\frac{1}{{n}^{2}}$倍 | |
| D. | 根据$\frac{GMm}{{r}^{2}}$=$\frac{m{v}^{2}}{r}$,可知卫星运动的线速度将增加到原来的$\frac{1}{n}$倍 |
6.关于宇宙速度,下列说法正确的是( )
| A. | 第一宇宙速度是人造地球卫星的最小发射速度,其等于地球赤道上物体的线速度 | |
| B. | 所有地球卫星的发射速度都大于或等于7.9 km/s | |
| C. | 第二宇宙速度是使物体挣脱太阳引力束缚的最小发射速度,其大小为11.2 km/s | |
| D. | 第三宇宙速度是使物体挣脱太阳引力束缚的最小发射速度,其大小为16.7 km/s |
3. 嫦娥奔月的过程可以简化为如图所示:“嫦娥一号”升空后,绕地球沿椭圆轨道运动,远地点A距地面高为h1,然后经过变轨被月球捕获,再经多次边轨,最终在距离月球表面高为h2的轨道上绕月球做匀速圆周运动,若已知地球的半径为R1,表面重力加速度为g0,月球的质量为M,半径为R2,引力常量为G,根据以上信息,可以确定( )
嫦娥奔月的过程可以简化为如图所示:“嫦娥一号”升空后,绕地球沿椭圆轨道运动,远地点A距地面高为h1,然后经过变轨被月球捕获,再经多次边轨,最终在距离月球表面高为h2的轨道上绕月球做匀速圆周运动,若已知地球的半径为R1,表面重力加速度为g0,月球的质量为M,半径为R2,引力常量为G,根据以上信息,可以确定( )
 嫦娥奔月的过程可以简化为如图所示:“嫦娥一号”升空后,绕地球沿椭圆轨道运动,远地点A距地面高为h1,然后经过变轨被月球捕获,再经多次边轨,最终在距离月球表面高为h2的轨道上绕月球做匀速圆周运动,若已知地球的半径为R1,表面重力加速度为g0,月球的质量为M,半径为R2,引力常量为G,根据以上信息,可以确定( )
嫦娥奔月的过程可以简化为如图所示:“嫦娥一号”升空后,绕地球沿椭圆轨道运动,远地点A距地面高为h1,然后经过变轨被月球捕获,再经多次边轨,最终在距离月球表面高为h2的轨道上绕月球做匀速圆周运动,若已知地球的半径为R1,表面重力加速度为g0,月球的质量为M,半径为R2,引力常量为G,根据以上信息,可以确定( )| A. | 月球表面的重力加速度 | B. | “嫦娥一号”在远地点A时的加速度 | ||
| C. | “嫦娥一号”绕月球运动的周期 | D. | “嫦娥一号”在远地点A时的速度 |
4.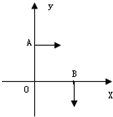 如图所示,一质点受一恒定合外力F作用从y轴上的A点平行于x轴射出,经过 一段时间到达x轴上的B点,在B点时其速度垂直于x轴指向y轴负方向,质点从A到B的过程,下列判断正确的是( )
如图所示,一质点受一恒定合外力F作用从y轴上的A点平行于x轴射出,经过 一段时间到达x轴上的B点,在B点时其速度垂直于x轴指向y轴负方向,质点从A到B的过程,下列判断正确的是( )
 如图所示,一质点受一恒定合外力F作用从y轴上的A点平行于x轴射出,经过 一段时间到达x轴上的B点,在B点时其速度垂直于x轴指向y轴负方向,质点从A到B的过程,下列判断正确的是( )
如图所示,一质点受一恒定合外力F作用从y轴上的A点平行于x轴射出,经过 一段时间到达x轴上的B点,在B点时其速度垂直于x轴指向y轴负方向,质点从A到B的过程,下列判断正确的是( )| A. | 合外力F可能向y轴负方向 | B. | 该质点的运动为匀变速运动 | ||
| C. | 该质点的速度大小可能保持不变 | D. | 该质点的速度一直在减小 |
 如图所示,两相同金属球放在光滑绝缘的水平面上,其中A球带9Q的正电荷,B球带Q的负电荷,由静止开始释放,经图示位置时,加速度大小均为a,然后发生碰撞,返回到图示位置时的加速度均为$\frac{16}{9}$a.
如图所示,两相同金属球放在光滑绝缘的水平面上,其中A球带9Q的正电荷,B球带Q的负电荷,由静止开始释放,经图示位置时,加速度大小均为a,然后发生碰撞,返回到图示位置时的加速度均为$\frac{16}{9}$a.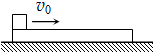 如图所示,质量为1kg的小物块以5m/s的初速度滑上一块原来静止在水平面上的木板,木板质量为4kg,木板与水平面间的动摩擦因数为0.02,经时间2s后,小物块从木板另一端以1m/s相对于地的速度滑出,g=10m/s2,求:
如图所示,质量为1kg的小物块以5m/s的初速度滑上一块原来静止在水平面上的木板,木板质量为4kg,木板与水平面间的动摩擦因数为0.02,经时间2s后,小物块从木板另一端以1m/s相对于地的速度滑出,g=10m/s2,求: