题目内容
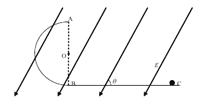
【题目】如图所示,在竖直平面内有xOy坐标系,长为l的不可伸长细绳,一端固定在A点,A点的坐标为(0、![]() ),另一端系一质量为m的小球。现在x坐标轴上(x>0)固定一个小钉,拉小球使细绳绷直并呈水平位置,再让小球从静止释放,当细绳碰到钉子以后,小球可以绕钉子在竖直平面内做圆周运动。
),另一端系一质量为m的小球。现在x坐标轴上(x>0)固定一个小钉,拉小球使细绳绷直并呈水平位置,再让小球从静止释放,当细绳碰到钉子以后,小球可以绕钉子在竖直平面内做圆周运动。
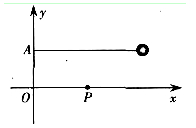
(1)当钉子在![]() 的P点时,小球经过最低点时细绳恰好不被拉断,求细绳能承受的最大拉力;
的P点时,小球经过最低点时细绳恰好不被拉断,求细绳能承受的最大拉力;
(2)为使小球释放后能绕钉子在竖直平面内做圆周运动,而细绳又不被拉断,求钉子所在位置的范围。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)当钉子在![]() 的P点时,小球绕钉子转动的半径为:
的P点时,小球绕钉子转动的半径为:
![]()
小球由静止到最低点的过程中机械能守恒: ![]()
在最低点细绳承受的拉力最大,有: ![]()
联解求得最大拉力![]() 。
。
(2)小球绕钉子圆周运动恰好到达最高点时,有: ![]()
运动中机械能守恒: ![]()
钉子所在位置为![]()
联解得![]()
因此钉子所在位置的范围为![]()

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目