题目内容
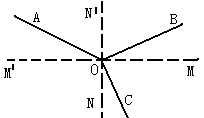
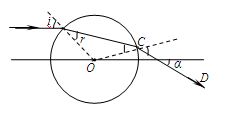
如图乙所示,MN是一条通过透明球体球心的直线.在真空中的单色细光束AB平行于MN射向球体,B为入射点,若出射光线CD与MN的交点P到球心O的距离是球半径的 倍,且与MN所成的角α=30°.求:透明体的折射率;
倍,且与MN所成的角α=30°.求:透明体的折射率;

 倍,且与MN所成的角α=30°.求:透明体的折射率;
倍,且与MN所成的角α=30°.求:透明体的折射率;
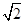
连接OB、BC,如图所示.
在B点光线的入射角、折射角分别标为i、r,在ΔOCP中:有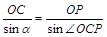
解得 ∠OCP=135°(45°值舍) ①(2分)
进而可得:∠COP=15°
由折射率定义:在B点有: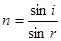 (2分)
(2分)
在C点有: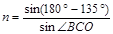 ,
,
又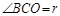
所以,i=45° ②(2分)
又: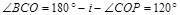 故:r=30° ③(2分)
故:r=30° ③(2分)
因此,透明体的折射率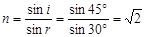 ④(2分)
④(2分)
在B点光线的入射角、折射角分别标为i、r,在ΔOCP中:有
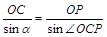
解得 ∠OCP=135°(45°值舍) ①(2分)
进而可得:∠COP=15°

由折射率定义:在B点有:
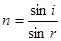 (2分)
(2分)在C点有:
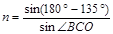 ,
,又
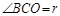
所以,i=45° ②(2分)
又:
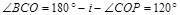 故:r=30° ③(2分)
故:r=30° ③(2分)因此,透明体的折射率
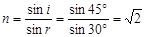 ④(2分)
④(2分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,这条光线从BC边射出棱镜后的光线与界面BC的夹角为( )
,这条光线从BC边射出棱镜后的光线与界面BC的夹角为( )
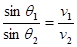 (式中
(式中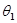 是入射角,
是入射角,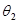 是折射角,
是折射角,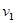 、
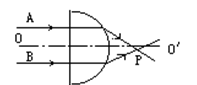
、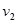 分别为超声波在肝外和肝内的传播速度),超声波在肿瘤表面发生反射时遵循的规律与光的反射规律相同。已知
分别为超声波在肝外和肝内的传播速度),超声波在肿瘤表面发生反射时遵循的规律与光的反射规律相同。已知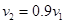 ,入射点与出射点之间的距离是d,入射角为i,肿瘤的反射面恰好与肝脏表面平行,则肿瘤离肝脏表面的深度h为( )
,入射点与出射点之间的距离是d,入射角为i,肿瘤的反射面恰好与肝脏表面平行,则肿瘤离肝脏表面的深度h为( )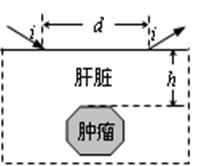
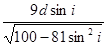
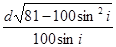
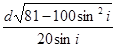
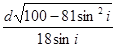


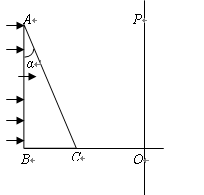
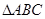 为一直角三棱镜的截面,其顶角
为一直角三棱镜的截面,其顶角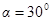 ,BC边长为a,棱镜的折射率为
,BC边长为a,棱镜的折射率为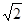 ,P为垂直于直线BCO的光屏。现有一宽度等于AB的平行单色光束垂直射向AB面,求在光屏P上被折射光线照亮的光带的宽度。
,P为垂直于直线BCO的光屏。现有一宽度等于AB的平行单色光束垂直射向AB面,求在光屏P上被折射光线照亮的光带的宽度。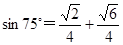 ;
;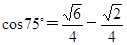 )
)