题目内容
可视为质点的小球A、B静止在光滑水平轨道上,A的左边固定有轻质弹簧,B与弹簧左端接触但不拴接,A的右边有一垂直于水平轨道的固定挡板P.左边有一小球C沿轨道以某一初速度射向B球,如图所示,C与B发生碰撞并立即结成一整体D,在它们继续向右运动的过程中,当D和A的速度刚好相等时,小球A恰好与挡板P发生碰撞,碰后A立即静止并与挡板P粘连.之后D被弹簧向左弹出,D冲上左侧与水平轨道相切的竖直半圆光滑轨道,其半径为R=0.6m,D到达最高点Q时,D与轨道间弹力F=2N.已知三小球的质量分别为mA=0.2kg、mB=mC=0.1kg.取g=10m/s2,求:
(1)D到达最高点Q时的速度vQ的大小
(2)D由Q点水平飞出后的落地点与Q点的水平距离s
(3)C球的初速度v0的大小.

(1)D到达最高点Q时的速度vQ的大小
(2)D由Q点水平飞出后的落地点与Q点的水平距离s
(3)C球的初速度v0的大小.

解 (1)D在Q点时据牛顿第二定律有F+mDg=mD
解得:vQ=
=
=2
(m/s)
(2)令D由Q点水平飞出后经时间t落至地面2R=
gt2 s=vQt
代入数据解得:s=
(m)
(3)C碰B,据动量守恒有:mCv0=(mC+mB)vD
解得:vD=
=
=
D向右压缩弹簧的过程中,据系统动量守恒:mDvD=(mD+mA)vA
解得:vA=
=
据机械能守恒:EP=
mDvD2-
(mD+mA)vA2
解得:EP=
A碰P静止后,D被弹簧向左弹出直到Q的过程中,据机械能守恒有:
mDvA2+EP=mDg?2R+
mDvQ2
代入数据解得:v0=8
(m/s)
答:
(1)D到达最高点Q时的速度vQ的大小为2
m/s.
(2)D由Q点水平飞出后的落地点与Q点的水平距离s为
m.
(3)C球的初速度v0的大小为8
m/s.
| vQ2 |
| R |
解得:vQ=
|
|
| 3 |
(2)令D由Q点水平飞出后经时间t落至地面2R=
| 1 |
| 2 |
代入数据解得:s=
6
| ||
| 5 |
(3)C碰B,据动量守恒有:mCv0=(mC+mB)vD
解得:vD=
| mCv0 |
| mC+mB |
| 0.1v0 |
| 0.1+0.1 |
| v0 |
| 2 |
D向右压缩弹簧的过程中,据系统动量守恒:mDvD=(mD+mA)vA
解得:vA=
| mDvD |
| mD+mA |
| v0 |
| 4 |
据机械能守恒:EP=
| 1 |
| 2 |
| 1 |
| 2 |
解得:EP=
| v02 |
| 80 |
A碰P静止后,D被弹簧向左弹出直到Q的过程中,据机械能守恒有:
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:v0=8
| 3 |
答:
(1)D到达最高点Q时的速度vQ的大小为2
| 3 |
(2)D由Q点水平飞出后的落地点与Q点的水平距离s为
6
| ||
| 5 |
(3)C球的初速度v0的大小为8
| 3 |

练习册系列答案
相关题目

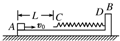
 平面上有一个长为L的木板B,上表面粗糙.在其左端有一个光滑的
平面上有一个长为L的木板B,上表面粗糙.在其左端有一个光滑的


