题目内容
19. 我国探月的“嫦娥”工程已启动,在不久的将来,我国宇航员将登上月球.假设探月宇航员站在月球表面一斜坡上的M点,并沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点N,斜面的倾角为θ,如图所示.将月球视为密度均匀、半径为r的球体,引力恒量为G,则月球的密度为( )
我国探月的“嫦娥”工程已启动,在不久的将来,我国宇航员将登上月球.假设探月宇航员站在月球表面一斜坡上的M点,并沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点N,斜面的倾角为θ,如图所示.将月球视为密度均匀、半径为r的球体,引力恒量为G,则月球的密度为( )| A. | $\frac{3{v}_{0}tanθ}{4πGt}$ | B. | $\frac{3{v}_{0}tanθ}{πGrt}$ | C. | $\frac{3{v}_{0}tanθ}{2πGrt}$ | D. | $\frac{{v}_{0}tanθ}{πGrt}$ |
分析 根据平抛运动规律列出水平方向和竖直方向的位移等式,结合几何关系求出重力加速度.
忽略地球自转的影响,根据万有引力等于重力列出等式.
根据密度公式求解.
解答 解:设该星球表面的重力加速度为g,根据平抛运动规律:
水平方向:x=v0t
竖直方向:y=$\frac{1}{2}$gt2
平抛位移与水平方向的夹角的正切值tanα=$\frac{y}{x}=\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$
得g=$\frac{2{v}_{0}tanθ}{t}$
设该星球质量M,对该星球表面质量为m1的物体有$\frac{GM{m}_{1}}{{r}^{2}}={m}_{1}g$
解得:$M=\frac{g{r}^{2}}{G}$
而V=$\frac{4}{3}π{r}^{3}$
则密度ρ=$\frac{M}{V}=\frac{3{v}_{0}tanθ}{2rGtπ}$
故C正确,ABD错误.
故选:C
点评 处理平抛运动的思路就是分解.重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9. 某物块从固定斜面底端以一定的初速度沿斜面上滑,其速度大小随时间变化的关系如图所示,则物块( )
某物块从固定斜面底端以一定的初速度沿斜面上滑,其速度大小随时间变化的关系如图所示,则物块( )
 某物块从固定斜面底端以一定的初速度沿斜面上滑,其速度大小随时间变化的关系如图所示,则物块( )
某物块从固定斜面底端以一定的初速度沿斜面上滑,其速度大小随时间变化的关系如图所示,则物块( )| A. | 在1.5 s时位移最大 | |
| B. | 沿斜面上滑的最大距离为2 m | |
| C. | 在1.5 s时回到斜面底端 | |
| D. | 上滑时加速度大小是下滑时加速度大小的2倍 |
7.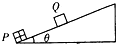 如图所示,固定的光滑绝缘斜面的底端固定着一个带正电的小物块P,将另一个带电小物块Q在斜面的某位置由静止释放,它将沿斜面向上运动.设斜面足够长,则在Q向上运动过程中( )
如图所示,固定的光滑绝缘斜面的底端固定着一个带正电的小物块P,将另一个带电小物块Q在斜面的某位置由静止释放,它将沿斜面向上运动.设斜面足够长,则在Q向上运动过程中( )
 如图所示,固定的光滑绝缘斜面的底端固定着一个带正电的小物块P,将另一个带电小物块Q在斜面的某位置由静止释放,它将沿斜面向上运动.设斜面足够长,则在Q向上运动过程中( )
如图所示,固定的光滑绝缘斜面的底端固定着一个带正电的小物块P,将另一个带电小物块Q在斜面的某位置由静止释放,它将沿斜面向上运动.设斜面足够长,则在Q向上运动过程中( )| A. | 加速度先减小后增大 | |
| B. | Q的电势能逐渐减小,机械能逐渐增大 | |
| C. | Q和P的电势能和重力势能之和逐渐减小 | |
| D. | Q和P的电势能和动能之和逐渐增大 |
8. 如图所示为一个正点电荷A与金属板B,C为A到B的垂线段的中点,D、E为该垂线段上的两点,DC=CE,下列说法正确的是( )
如图所示为一个正点电荷A与金属板B,C为A到B的垂线段的中点,D、E为该垂线段上的两点,DC=CE,下列说法正确的是( )
 如图所示为一个正点电荷A与金属板B,C为A到B的垂线段的中点,D、E为该垂线段上的两点,DC=CE,下列说法正确的是( )
如图所示为一个正点电荷A与金属板B,C为A到B的垂线段的中点,D、E为该垂线段上的两点,DC=CE,下列说法正确的是( )| A. | 正点电荷A在金属板B内部产生的电场强度为零 | |
| B. | D点的电场强度大于E点的电场强度 | |
| C. | D、C两点间的电势差大于C、E两点间的电势差 | |
| D. | 只在电场力作用下,电子从E点沿直线运动到D点,电子在CD段动能的变化小于在CE段动能的变化 |
 如图所示,水平放置的汽缸内壁光滑,在 B处设有限制装置,使活塞在B处不能向左运动,B左侧气缸的容积为V0,A、B之间的容积为0.5V0.开始时活塞在B处,缸内气体的压强为0.9p0(p0为大气压强),保持温度不变,设法使活塞移至A处,此时缸内气体的压强p=0.6p0,若欲保持缸内气体的压强p不变,再使活塞由A回到B,可通过降低温度实现.(选填“升高”或“降低”)
如图所示,水平放置的汽缸内壁光滑,在 B处设有限制装置,使活塞在B处不能向左运动,B左侧气缸的容积为V0,A、B之间的容积为0.5V0.开始时活塞在B处,缸内气体的压强为0.9p0(p0为大气压强),保持温度不变,设法使活塞移至A处,此时缸内气体的压强p=0.6p0,若欲保持缸内气体的压强p不变,再使活塞由A回到B,可通过降低温度实现.(选填“升高”或“降低”) 如图所示,倾角为45°的粗糙斜面AB底端与半径R=0.4m的光滑半圆轨道BC平滑相接,O为轨道圆心,BC为圆轨道直径且处于竖直平面内,A、C两点等高.质量m=1kg的滑块(可视为质点)从A点由静止开始下滑,恰能滑到与O等高的D点,g取10m/s2.
如图所示,倾角为45°的粗糙斜面AB底端与半径R=0.4m的光滑半圆轨道BC平滑相接,O为轨道圆心,BC为圆轨道直径且处于竖直平面内,A、C两点等高.质量m=1kg的滑块(可视为质点)从A点由静止开始下滑,恰能滑到与O等高的D点,g取10m/s2.