��Ŀ����
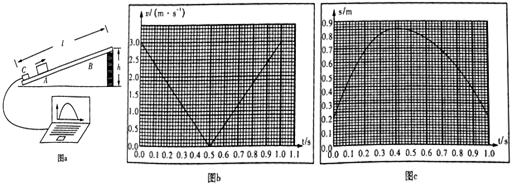
14�� ��ͼ��ʾ�����Ϊ45��Ĵֲ�б��AB����뾶R=0.4m�Ĺ⻬��Բ���BCƽ����ӣ�OΪ���Բ�ģ�BCΪԲ���ֱ���Ҵ�����ֱƽ���ڣ�A��C����ȸߣ�����m=1kg�Ļ��飨����Ϊ�ʵ㣩��A���ɾ�ֹ��ʼ�»���ǡ�ܻ�����O�ȸߵ�D�㣬gȡ10m/s2��
��ͼ��ʾ�����Ϊ45��Ĵֲ�б��AB����뾶R=0.4m�Ĺ⻬��Բ���BCƽ����ӣ�OΪ���Բ�ģ�BCΪԲ���ֱ���Ҵ�����ֱƽ���ڣ�A��C����ȸߣ�����m=1kg�Ļ��飨����Ϊ�ʵ㣩��A���ɾ�ֹ��ʼ�»���ǡ�ܻ�����O�ȸߵ�D�㣬gȡ10m/s2����1����ʹ�����ܵ���C�㣬�����ٴ���ض�ߴ��ɾ�ֹ��ʼ�»���
��2���������뿪C����ǡ�ܴ�ֱ����б���ϣ��龭��C��ʱ�Թ����ѹ����
��3����ʹ������Բ����BDC�β�����������A�»��ĸ߶�Ӧ������ʲô������
���� ��1����A��D�Ĺ����и��ݶ��ܶ������Ħ�������������ܵ���C�㣬����ţ�ٵڶ��������C����ٶȣ����ݶ��ܶ�����ø߶�
��2��С���C����ƽ���˶�������ƽ���˶����ص㣬���C����ٶȣ�����ţ�ٵڶ�������öԹ����ѹ����
��3�����岻�����������ڹ������ͨ����ߵ�պõ���D�㼴��
��� �⣺��1����A��D�����ݶ��ܶ����ɵ�
mg��2R-R��-��mgcos45��$\frac{2R}{{sin{{45}��}}}$=0
��æ�=0.5
������ǡ�ܵ���C�㣬$mg=\frac{{mv}_{C}^{2}}{R}$
��${v}_{C}=\sqrt{gR}=2m/s$
�Ӹ�ΪH����ߵ㵽C�Ĺ��̣�
���ݶ��ܶ��� mg��H-2R��-��mgcos45��$\frac{H}{{sin{{45}��}}}$=$\frac{1}{2}mv_c^2$
���H=2m
��2���뿪C�����ƽ���˶�����ֱ��б����ʱ��
x=vCt
$y=\frac{1}{2}g{t}^{2}=\frac{{v}_{y}}{2}t$
$tan45��=\frac{{v}_{C}}{{v}_{y}}$
$tan45��=\frac{2R-y}{x}$
��� ${v}_{c}=\frac{4\sqrt{3}}{3}m/s$
��C�㣬����ţ�ٵڶ������� $mg+{F}_{N}=\frac{{mv}_{C}^{2}}{R}$
��ã�FN=3.3N
��ţ�ٵ������ɿ�֪������Թ����ѹ��ΪF��N=FN=3.3N
������ֱ����
��3���������֪�������A�����������߶�Ϊ2R=0.8m���»�ǡ�õ���D�㣬���ԣ���ʹ������Բ����BDC�β�����������A�»��ĸ߶�h��2m��h��0.8m
�𣺣�1����ʹ�����ܵ���C�㣬�������ٴ����2m�ߴ��ɾ�ֹ��ʼ�»���
��2���������뿪C����ǡ�ܴ�ֱ����б���ϣ����龭��C��ʱ�Թ����ѹ��Ϊ3.3N��
��3����ʹ������Բ����BDC�β�����������A�»��ĸ߶�Ӧ������h��2m��h��0.8m
���� �����Ƕ��ܶ�������������ƽ���˶�������֪ʶ���ۺϣ��ؼ�Ҫע���ھ��������ٽ�������֪��С��ͨ����ֱƽ��Բ�����ߵ�ʱ������ǡ���ṩ������������ƽ���˶���Ҫ��ϼ���֪ʶ�������

��1����Ҫ�������У�����ʱ��������ľ�塢����дֽƬ��4-6V��ѹ�����Դ��ֽ�����̶ȳ�
��2������˵����ȷ����B
A���϶�ֽ����ͬʱ���պϵ�Դ����
B���ȱպϵ�Դ���أ��ô���ʱ����������ʱ���϶�ֽ��
C��ֽ���ϵĴ���ܼ�˵����ֽ���˶��ٶȽϴ�
D�����ô����ֽ������ȷ���������ijЩ��ʱֽ���˶���˲ʱ�ٶ�
��3��ijͬѧ�϶�ֽ���˶�������ʱ����ֽ���ϴ��һϵ�е㣬����ʱÿ��1����ȡһ�������㣬������ĸA��B��C��D��E��F��
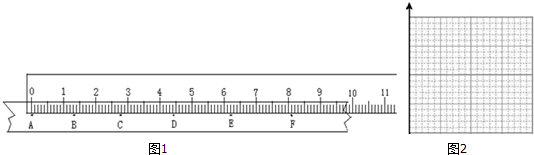
��ͼ1��ʾ��ijͬѧ��mm�̶ȳ߽��в��������æ����B��C��D��F�ڿ̶ȳ��ϵ�λ�ã�����У�
| ������ | B | C | D | E | F |
| λ�ã�cm�� | 4.44 | 6.22 | 8.12 |
��4������Ϊһ��ʱ���м�ʱ�̵�˲ʱ�ٶȾ������ʱ���ڵ�ƽ���ٶȣ������ʱ������C��ʱС�����ٶ�VC=0.388m/s��С����C���˶�D������еļ��ٶ�a=1.00m/s2��
��5����ͼ2��������ֽ�Ͻ������꣬����ֽ���˶��Ĵ���B��E����ٶ�-ʱ��ͼ��v-tͼ���Ӵ���A�㿪ʼ��ʱ����
| A�� | �糡ǿ�ȵĴ�С������ɵĵ��������� | |
| B�� | һ������ɼ����ĵ糡������ǿ�糡 | |
| C�� | ͬһ�糡�����ڣ��糡��Խ�ܴ����糡��Խǿ | |
| D�� | �糡�м����ɵ�����������ǵ糡ǿ�ȵķ��� |
 �ҹ�̽�µġ��϶𡱹������������ڲ��õĽ������ҹ��Ա������������̽���Ավ���������һб���ϵ�M�㣬����ˮƽ�����Գ��ٶ�v0�׳�һ��С���С��ʱ��t�䵽б������һ��N��б������Ϊ�ȣ���ͼ��ʾ����������Ϊ�ܶȾ��ȡ��뾶Ϊr�����壬��������ΪG����������ܶ�Ϊ��������
�ҹ�̽�µġ��϶𡱹������������ڲ��õĽ������ҹ��Ա������������̽���Ավ���������һб���ϵ�M�㣬����ˮƽ�����Գ��ٶ�v0�׳�һ��С���С��ʱ��t�䵽б������һ��N��б������Ϊ�ȣ���ͼ��ʾ����������Ϊ�ܶȾ��ȡ��뾶Ϊr�����壬��������ΪG����������ܶ�Ϊ��������| A�� | $\frac{3{v}_{0}tan��}{4��Gt}$ | B�� | $\frac{3{v}_{0}tan��}{��Grt}$ | C�� | $\frac{3{v}_{0}tan��}{2��Grt}$ | D�� | $\frac{{v}_{0}tan��}{��Grt}$ |
��1��������ļ��ٶȵĴ�С��
��2��������λ�ƵĴ�С
| t/s | 0 | 100 | 300 | 400 | 500 | 550 | 600 |
| v/m•s-1 | 30 | 40 | 50 | 50 | 60 | 70 | 80 |
 ��ͼ��ʾ��������һЩ���ߺ��ĸ���ֵ��ͬ�ĵ�����ɵĵ�·��������A��B��C��D�ĸ�����������֪������������ֵ�����¹�ϵ��RAB=2RAC��RCD=2RAB��RAC=RBD�����ں��ڻ�����·ͼ��
��ͼ��ʾ��������һЩ���ߺ��ĸ���ֵ��ͬ�ĵ�����ɵĵ�·��������A��B��C��D�ĸ�����������֪������������ֵ�����¹�ϵ��RAB=2RAC��RCD=2RAB��RAC=RBD�����ں��ڻ�����·ͼ��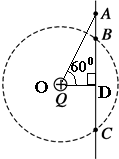 ��ͼ��ʾ���⻬��Եϸ����ֱ���ã������������QΪԲ�ĵ�ijԲ����B��C���㣬����Ϊm���������Ϊ+q���п�С��Ӹ���A�����ٶ��»���AB=h��OD=d��OD��AC����AOD=60�㣬С��B��ʱ���ٶȴ�СΪ$\sqrt{gh}$����
��ͼ��ʾ���⻬��Եϸ����ֱ���ã������������QΪԲ�ĵ�ijԲ����B��C���㣬����Ϊm���������Ϊ+q���п�С��Ӹ���A�����ٶ��»���AB=h��OD=d��OD��AC����AOD=60�㣬С��B��ʱ���ٶȴ�СΪ$\sqrt{gh}$����