题目内容
10．如图所示皮带转动轮，大轮直径是小轮直径的2倍，A是大轮边缘上一点，B是小轮边缘上一点，C是大轮上一点，C到圆心O1的距离等于小轮半径．转动时皮带不打滑，则A、B、C三点的角速度之比ωA：ωB：ωC=1：2：1．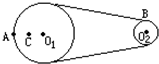
分析 共轴转动，角速度相等，靠传送带传动，轮子边缘上的点线速度相等，结合线速度与角速度的关系即可得出角速度之比．
解答 解：A、B两点是靠传送带传动轮子边缘上的点，线速度相等，因为大轮的半径是小轮半径的2倍，根据v=rω，知ωA：ωB=1：2，因为A、C共轴转动，则角速度相等，所以ωA：ωB：ωC=1：2：1．
故答案为：1：2：1
点评 解决本题的关键知道共轴转动的质点角速度相等，靠传送带传动轮子边缘上的点线速度大小相等．知道线速度、角速度、向心加速度之间的大小关系．
练习册系列答案
相关题目
20．
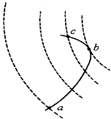如图所示，虚线表示等势面，相邻两等势面间的电势差相等，有一带正电小球在该电场中运动，不计小球所受的重力和空气阻力，实线表示该小球的运动轨迹．已知小球在a点的动能等于29eV，运动到b点时的动能等于2eV，若取C点为零电势点，则这个带电小球的电势能等于-6eV时，它的动能等于（ ）
如图所示，虚线表示等势面，相邻两等势面间的电势差相等，有一带正电小球在该电场中运动，不计小球所受的重力和空气阻力，实线表示该小球的运动轨迹．已知小球在a点的动能等于29eV，运动到b点时的动能等于2eV，若取C点为零电势点，则这个带电小球的电势能等于-6eV时，它的动能等于（ ）| A． | 33eV | B． | 24eV | C． | 12eV | D． | 17ev |
18．物体以v0的速度水平抛出，当竖直分位移与水平分位移大小相等时，以下说法正确的是（ ）
| A． | 瞬时速度的大小为$\sqrt{5}{v_0}$ | |
| B． | 此时小球速度的方向与位移的方向相同 | |
| C． | 运动时间为$\frac{v_0}{g}$ | |
| D． | 运动位移的大小为$\frac{{2\sqrt{2}v_0^2}}{g}$ |
5．物体在运动过程中，克服重力做功为50J，则（ ）
| A． | 重力做功为50 J | B． | 物体的重力势能一定减少50 J | ||
| C． | 物体的重力势能可能增加40 J | D． | 重力做了50 J的负功 |
15．把自由落体运动下落的总高度分成相等的三段，按从上到下的顺序，物体在这三段距离的平均速度之比等于（ ）
| A． | 1：3：5 | B． | $1：（\sqrt{2}+1）：（\sqrt{2}+\sqrt{3}）$ | C． | $1：\sqrt{2}：\sqrt{3}$ | D． | 1：4：9 |
19．下列有关高中物理实验的说法中，正确的是（ ）
| A． | “验证力的平行四边形定则”实验中，同一次实验用两个弹簧秤拉和只用一个弹簧秤拉时，结点要拉到同一位置 | |
| B． | 电磁打点计时器的工作电压是220V的交流电 | |
| C． | 在用打点计时器“研究匀变速直线运动”的实验中，由纸带上的一系列点迹取计数点，可求出任意两个计数点之间的平均速度 | |
| D． | 在“探究加速度与物体所受合力F及质量m的关系”实验中应控制砂和砂桶的质量远小于小车和小车上的砝码质量． |
12．光在科学技术、生产和生活中有着广泛的应用，下列说法正确的是（ ）
| A． | 用透明的标准平面样板检查光学平面的平整程度是利用光的干涉现象 | |
| B． | 用三棱镜观察白光看到的彩色图样是利用光的衍射现象 | |
| C． | 利用红外遥感技术测量远处物体的温度 | |
| D． | 光子说和玻尔原子模型都体现了量子化理论 |