题目内容
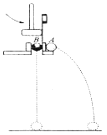
【题目】如图所示,在磁感应强度大小为B、方向竖直向上的匀强磁场中,有一上、下两层均与水平面平行的“U”形光滑金属导轨,在导轨面上各放一根完全相同的质量为m的匀质金属杆A1和A2,开始时两根金属杆位于同一竖直面内且杆与轨道垂直。设两导轨面相距为H,导轨宽为L,导轨足够长且电阻不计,金属杆单位长度的电阻为r。现有一质量为![]() 的不带电小球以水平向右的速度v0撞击杆A1的中点,撞击后小球反弹落到下层面上的C点。C点与A2杆初始位置相距为s。重力加速度大小为g。求:
的不带电小球以水平向右的速度v0撞击杆A1的中点,撞击后小球反弹落到下层面上的C点。C点与A2杆初始位置相距为s。重力加速度大小为g。求:
(1)回路内感应电流的最大值;
(2)整个运动过程中感应电流最多产生了多少热量;
(3)当杆A2与杆A1的速度比为1∶3时,A2受到的安培力大小。

【答案】(1)  (2)
(2)  (3)
(3)
【解析】
(1)小球撞击杆过程动量守恒,之后做平抛运动。设小球碰撞后速度大小为v1,杆获得的速度大小为v2,则有
0.5mv0=0.5m(-v1)+mv2
s=v1t
H=![]() gt2
gt2
所以
![]()
回路内感应电动势的最大值为E1=BLv2,电阻R=2Lr
故杆在磁场中运动的最大电流

(2)两金属杆在磁场中运动始终满足动量守恒,设两杆最终速度为v′,则
mv2=2mv′
感应电流最多产生的热量为
![]()
代入v2和v′计算得

(3)设杆A2和杆A1的速度大小为v、3v,则根据动量守恒定律得
mv2=mv+m·3v
由法拉第感应定律和右手定则得此时回路的总感应电动势为
E2=BL(3v-v)
感应电流
![]()
安培力
F=BIL
联合以上各式得


练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目