题目内容
14.某商场有一自动扶梯,某客户沿向上开动的自动扶梯走上楼时,数得走了21级楼梯;当他以同样的速度(相对电梯)沿向上开动的自动扶梯走下楼时,数得走了42级楼梯,则该自动扶梯的级数为28级.分析 设人的速度为v1,自动扶梯的速度为v2,自动扶梯总级数为N,上楼时间为t1,则人的速度乘以上楼时的时间加上自动扶梯的速度乘以上楼时的时间就等于自动扶梯总级数N;
设下楼时间为t2,则人的速度乘以下楼时的时间减去电梯的速度乘以下楼时的时间就等于自动扶梯总级数N;
根据以上分析,列出方程解答.
解答 解:设v1为人的速度,v2为电梯的速度,自动扶梯总级数为N,上楼时,时间为t1,每一级台阶长度为l;
则v1t1+v2t1=Nl,v1t1=N1l
下楼时,时间为t2,
v1t2-v2t2=Nl,v1t2=N2l
联立解得:N=$\frac{2{N}_{1}{N}_{2}}{{N}_{1}+{N}_{2}}$
由题意知:N1=21,N2=42,则自动扶梯级数N=$\frac{2{N}_{1}{N}_{2}}{{N}_{1}+{N}_{2}}$=28级.
故答案为:28.
点评 解答此题的关键是要明确人的速度要快于自动扶梯的速度,否则他就下不来,此题的难点在于解方程,因此要求学生具备一定的学科综合能力.

练习册系列答案
相关题目
2.如图为AB两人在同一直线上运动的位移图象,图象表示( )
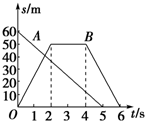

| A. | A、B两人在第5秒末相遇 | B. | A、B两人在第5秒内同向而行 | ||
| C. | 在5秒内,A走的位移比B走的位移大 | D. | 在5秒内,A走的路程比B走的路程大 |
9.一直向前作直线运动的小球在第1s内通过1m,在第2s内通过2m,在第3s内通过3m,在第4s内通过4m,下面有关小球运动的描述,正确的是( )
| A. | 小球在这4s内的平均速度是2.5 m/s | |
| B. | 小球在第3s、第4s两秒内的平均速度是3.5 m/s | |
| C. | 小球在第3s末的瞬时速度是3 m/s | |
| D. | 小球在第4s内的平均速度是1m/s |
19.从“嫦娥奔月”的美丽传说,到“飞天壁画”上的婀娜身影;从战国时期屈原面向长空的“天问”,到明代万户乘坐绑在一起的火箭开始人类飞向空中的首次尝试,2011年9月29日,中国在酒泉卫星发射中心用长征二号F运载火箭将天宫一号目标飞行器发射升空.北京时间11月1日清晨5时58分07秒,中国“长征二号F”遥八运载火箭在酒泉卫星发射中心载人航天发射场点火发射,火箭飞行583秒后,将“神舟八号”飞船成功送入近地点200公里、远地点330公里的预定轨道,之后,我国还将连续发射“神九”、“神十”飞船与天宫一号交会对接,从而建立第一个中国空间实验室.这个神话将在中国实现.已知地球和月球的质量分别为M1和M2,月球半径为R,月球绕地球公转的轨道半径为r,引力常量为G,假设已探测到在月球的环境温度下,水蒸气分子无规则热运动的平均速率为v.则( )
| A. | 月球表面重力加速度为G$\frac{{M}_{2}}{{R}^{2}}$ | |
| B. | 月球表面重力加速度为G$\frac{M_1}{r^2}$ | |
| C. | 若$\frac{{v}^{2}}{R}$>G$\frac{{M}_{2}}{{R}^{2}}$,就表明月球表面无水 | |
| D. | 若$\frac{{v}^{2}}{R}$>G$\frac{{M}_{2}}{{r}^{2}}$,就表明月球表面无水 |
6.某同学设计了一个探究加速度a与物体所受合力F及质量M关系的实验,图(a)为实验装置简图.(交流电的频率为50Hz)
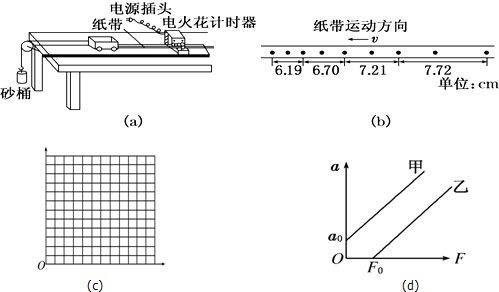
(1)图(b)所示为某次实验得到的纸带,根据纸带可求出小车的加速度大小为3.2m/s2.(保留两位有效数字)
(2)若取小车质量M=0.4kg,改变砂桶和砂的质量m的值,进行多次实验,以下m的值不合适的是BD(多选题).
A.m1=5g B.m2=1kg C.m3=10g D.m4=400g
(3)为了用细线的拉力表示小车受到的合外力,实验操作时必须首先平衡小车的摩擦力,该操作是否成功,判断的依据是不挂砂桶时,小车在倾斜的木板上是否匀速运动.
(4)某同学在做加速度和力、质量的关系的实验中,测得小车的加速度a和拉力F的数据如表所示:
①根据表中的数据在图(c)示的坐标中作出a-F图象;
②若甲、乙两同学在实验过程中,由于没有按照正确步骤进行实验,处理数据后得出如图(d)所示的a-F图象.试分析甲、乙两同学可能存在的问题:
甲:平衡摩擦力时把长木板抬得过高
乙:没有平衡摩擦力或平衡摩擦力不足.

(1)图(b)所示为某次实验得到的纸带,根据纸带可求出小车的加速度大小为3.2m/s2.(保留两位有效数字)
(2)若取小车质量M=0.4kg,改变砂桶和砂的质量m的值,进行多次实验,以下m的值不合适的是BD(多选题).
A.m1=5g B.m2=1kg C.m3=10g D.m4=400g
(3)为了用细线的拉力表示小车受到的合外力,实验操作时必须首先平衡小车的摩擦力,该操作是否成功,判断的依据是不挂砂桶时,小车在倾斜的木板上是否匀速运动.
(4)某同学在做加速度和力、质量的关系的实验中,测得小车的加速度a和拉力F的数据如表所示:
| F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| a/(m•s-2) | 0.11 | 0.19 | 0.29 | 0.40 | 0.51 |
②若甲、乙两同学在实验过程中,由于没有按照正确步骤进行实验,处理数据后得出如图(d)所示的a-F图象.试分析甲、乙两同学可能存在的问题:
甲:平衡摩擦力时把长木板抬得过高
乙:没有平衡摩擦力或平衡摩擦力不足.
3.把电热器接到110V的直流电源上,每秒产生的热量为Q,现把它接到正弦交流电源E,每秒产生的热量也为Q,则交流电压的最大值是( )
| A. | 110$\sqrt{2}$v | B. | 220$\sqrt{2}$V | C. | 220V | D. | 110V |
4.在水平铁路转弯处,往往使外轨略高于内轨,对这种做法说法错误的是( )
| A. | 减轻火车轮子挤压外轨 | |
| B. | 减轻火车轮子挤压内轨 | |
| C. | 使火车车身倾斜,利用重力和支持力的合力提供转弯所需向心力 | |
| D. | 限制火车向外脱轨 |
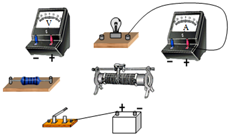 有一个标有“2.5V 0.3A”字样的小灯泡,现要测定其在0到2.5V的区间内不同电压下的电2,4,6功率,并作出其电功率P与其两端电压的平方U2的关系曲线.有下列器材可供选择:
有一个标有“2.5V 0.3A”字样的小灯泡,现要测定其在0到2.5V的区间内不同电压下的电2,4,6功率,并作出其电功率P与其两端电压的平方U2的关系曲线.有下列器材可供选择: