题目内容
20. 如图所示,质量为m的小物体用不可伸长的轻细线悬挂在天花板上,处于静止状态.现对处于静止状态的物体施加一个大小为F、与竖直方向夹角为θ的斜向上恒定拉力,平衡时细线与竖直方向的夹角为60°;保持拉力大小和方向不变,仅将小物体的质量增为2m,再次平衡时,细线与竖直方向的夹角为30°,重力加速度为g,则( )
如图所示,质量为m的小物体用不可伸长的轻细线悬挂在天花板上,处于静止状态.现对处于静止状态的物体施加一个大小为F、与竖直方向夹角为θ的斜向上恒定拉力,平衡时细线与竖直方向的夹角为60°;保持拉力大小和方向不变,仅将小物体的质量增为2m,再次平衡时,细线与竖直方向的夹角为30°,重力加速度为g,则( )| A. | F=mg | B. | $F=\frac{{\sqrt{3}}}{2}mg$ | C. | θ=30° | D. | θ=60° |
分析 以物体为研究对象,画出受力示意图,两种情况下根据正弦定理列方程求解.
解答 解:以物体为研究对象,设平衡时绳子与竖直方向的夹角为α,受力情况如图所示,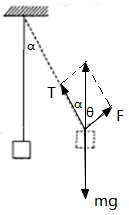
当物体重力为mg时,α=60°,根据正弦定理可得:$\frac{F}{sin60°}=\frac{mg}{sin(180°-60°-θ)}$,即$\frac{F}{sin60°}=\frac{mg}{sin(120°-θ)}$,
当物体的重力为2mg时,α=30°,根据正弦定理可得:$\frac{F}{sin30°}=\frac{mg}{sin(180°-30°-θ)}$,即$\frac{F}{sin30°}=\frac{mg}{sin(150°-θ)}$,
联立解得:θ=60°,F=mg;所以AD正确,BC错误;
故选:AD.
点评 本题主要是考查了共点力的平衡问题,解答此类问题的一般步骤是:确定研究对象、进行受力分析、利用平行四边形法则进行力的合成或者是正交分解法进行力的分解,然后在坐标轴上建立平衡方程进行解答.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
10. 如图所示,粗糙斜面固定在水平面上,轻质弹簧一端固定在斜面顶端,另一端与小物块相连,弹簧处于自然长度时物块位于O点且恰好处于静止状态.现将物块从O点拉至A点,撤去拉力后物块由静止向上运动,经O点到达B点时速度为零,则物块从A运动到B的过程中( )
如图所示,粗糙斜面固定在水平面上,轻质弹簧一端固定在斜面顶端,另一端与小物块相连,弹簧处于自然长度时物块位于O点且恰好处于静止状态.现将物块从O点拉至A点,撤去拉力后物块由静止向上运动,经O点到达B点时速度为零,则物块从A运动到B的过程中( )
 如图所示,粗糙斜面固定在水平面上,轻质弹簧一端固定在斜面顶端,另一端与小物块相连,弹簧处于自然长度时物块位于O点且恰好处于静止状态.现将物块从O点拉至A点,撤去拉力后物块由静止向上运动,经O点到达B点时速度为零,则物块从A运动到B的过程中( )
如图所示,粗糙斜面固定在水平面上,轻质弹簧一端固定在斜面顶端,另一端与小物块相连,弹簧处于自然长度时物块位于O点且恰好处于静止状态.现将物块从O点拉至A点,撤去拉力后物块由静止向上运动,经O点到达B点时速度为零,则物块从A运动到B的过程中( )| A. | 物块在位置B点时,处于平衡状态 | |
| B. | 当A点离O点越远时,物块所能达到的最大动能的位置也离O点越远 | |
| C. | 从O向B运动过程中,物块的加速度逐渐减小 | |
| D. | 从A向O运动过程中,系统的弹性势能的减少量大于机械能的增加量 |
8.下列说法中正确的是( )
| A. | 悬浮在水中的花瓣颗粒的布朗运动反应了花粉分子的无规则热运动 | |
| B. | 在轨道上运行的航天器内小水滴呈球形是水的表面张力作用的结果 | |
| C. | 封闭容器中气体压强是由于气体受到重力而产生的,所以做自由落体运动的容器内气体压强为零 | |
| D. | 油膜法测分子直径的实验中,将油膜的厚度作为分子的直径 | |
| E. | 密闭、绝热的气缸中的理想气体对外做功时,其温度一定会降低 |
15.下列说法中正确的是( )
| A. | 浸润和不浸润现象都是分子力作用的表现 | |
| B. | 液晶既具有液体的流动性,又像某些晶体那样具有光学各向异性 | |
| C. | 熵增加原理说明一切自然过程总是向着分子热运动的无序性减少的方向进行 | |
| D. | 在相对湿度比较大的时候,较低的温度就能引起中暑,是因为汗液不容易蒸发 | |
| E. | 在温度不变的情况下,增大液面上方饱和汽的体积,待气体重新达到饱和时,饱和汽的压强增大 |
12.某质点沿直线运动,其速度时间图象,如图所示,下列说法不正确的是( )
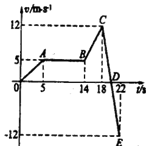

| A. | D 点对应时刻离出发点最远 | |
| B. | 质点的总位移为 90.5m | |
| C. | BC 段与 CD 段质点的加速度之比为$\frac{7}{24}$ | |
| D. | CE 段对应过程的加速度最大 |
 如图所示为一置于空气中用透明材料做成的圆柱体元件的横截面,AB为通过横截面圆心O的轴线,横截面的半径为R,一平行于AB的细光束从N点射入该元件,射出后与直线AB交于P点,现测得MN与AB的距离为$\frac{\sqrt{3}}{2}$R,OP=$\sqrt{3}$R,求:
如图所示为一置于空气中用透明材料做成的圆柱体元件的横截面,AB为通过横截面圆心O的轴线,横截面的半径为R,一平行于AB的细光束从N点射入该元件,射出后与直线AB交于P点,现测得MN与AB的距离为$\frac{\sqrt{3}}{2}$R,OP=$\sqrt{3}$R,求:
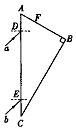 如图所示,一玻璃砖的截面为直角三角形ABC,其中∠A=60°,AB=9cm,现有两细束平行且相同的单色光a、b,分别从AC边上的D点、E点以45°角入射,且均能从AB边上的F点射出,已知AD=AF=3cm,求:
如图所示,一玻璃砖的截面为直角三角形ABC,其中∠A=60°,AB=9cm,现有两细束平行且相同的单色光a、b,分别从AC边上的D点、E点以45°角入射,且均能从AB边上的F点射出,已知AD=AF=3cm,求: 质量为1kg的小物块在一水平恒力F1作用下由静止开始在粗糙水平面上做直线运动,10s末将F1变为与F1方向相同的恒力F2,40s末撤去力F2,0-60s内小物体的加速度随时间变化的图线如图所示.
质量为1kg的小物块在一水平恒力F1作用下由静止开始在粗糙水平面上做直线运动,10s末将F1变为与F1方向相同的恒力F2,40s末撤去力F2,0-60s内小物体的加速度随时间变化的图线如图所示.