��Ŀ����
����Ŀ���⻬��Ե��������ֱƽ��Ľ����������ߣ���ͼ��ʾ�������ߵķ�����y=x2���°벿����һ��ˮƽ�������ǿ�ų��У��ų����ϱ߽���y=a��ֱ�ߣ�ͼ�е�������ʾ����һ������Ϊm��С���������������y=b��b��a�����������������»������Կ����������������ٶ�ֵΪg��������
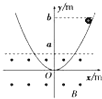
A.С���������������»�������ͣ��O��
B.С���������������»����O��ѹ��һ������mg
C.С���������������»���ÿ�ι�O���ٶ�һֱ�ڼ�С
D.С���������������»������ղ����Ľ�����������mg��b��a��
���𰸡�BD
��������
A��Բ���ڴų����˶��Ĺ����У�û�и�Ӧ��������е�ܲ��ټ�С������Բ��������ֱ��y=a�������ذڶ�����A����
B��С���������������»�������͵�Oֻ�ܵ�������֧���������ã������ṩ�����������ٶȵķ������ϣ����ԶԹ����ѹ��һ������mg����B��ȷ��
C��Բ����е�ܲ��ټ�Сʱ��������ֱ��y=a�������ذڶ���֮��ÿ�ι�O���ٶȲ��ټ�С����C����
D��Բ���ڴų����˶��Ĺ����У�û�и�Ӧ��������е�ܲ��ټ�С������Բ��������ֱ��y=a�������ذڶ���С���������������»������ղ����Ľ������������ڼ��ٵĻ�е�ܣ���
![]()
��D��ȷ��
��ѡBD��