题目内容
【题目】甲乙两人做抛球游戏,如图所示,甲站在一辆平板车上,车与水平地面间的摩擦不计。甲与车的总质量M=50kg,另有一质量m=2kg的球,乙站在车对面的地上,身旁有若干质量不等的球。开始车静止,甲将球以速度v(相对于地面)水平抛给乙,乙接到抛来的球后,马上将另一只质量为m/=2m的球以相同速率v水平抛回给甲,甲接到球后,再以速率v将此球水平抛给乙,这样反复进行,乙每次抛回给甲的球的质量都等于他接到球的质量的2倍,求:
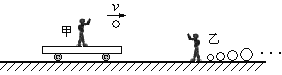
(1)甲第一次抛出球后,车的速度多大?
(2)甲第二次抛出球后,车的速度多大?
(3)从第一次算起,甲抛出多少个球后,再不能接到乙抛回来的球。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
根据动量守恒即可求出车的速度;对于甲和小车整体,每次接到球并抛出后,甲和小车整体的动量均增加,增加量等于小球动量的2倍,结合动量守恒定律分析即可。
(1)以甲和车及第一个球为系统,选向右为正方向,设甲第一次抛出球后的后退速度为v1,由动量守恒得0=mv-Mv1
解得:![]()
(2)再以甲和车及抛回来的球为系统,设甲第二次抛球的速度为v2,甲接到一个从右方抛过来的质量为2m的球,接着又向右扔回一个质量为2m的球,
此过程应用动量守恒得-Mv1 -2mv= -Mv2+2mv
整理可得:Mv2 =4mv+Mv1
解得:![]() ,方向向左
,方向向左
(3)第1个球抛出后甲和小车整体的动量为:mv0;
第2个球抛出后甲和小车整体的动量为:mv0+2mv0;
第3个球抛出后甲和小车整体的动量为:mv0+2mv0+4mv0;
…
第n个球抛出后甲和小车整体的动量为:mv0+2mv0+4mv0+…+2nmv0=(M+nm)vn
同时要满足:vn≤v0
解得:n>4,故n最大取5
即从第一次起,甲抛出5个球后,再也不能接到乙抛回来的球