题目内容
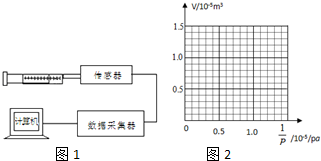
(2012?长宁区二模)用DIS测量不规则固体的密度,实验装置如图1所示.实验步骤如下:
Ⅰ.将质量为9.30×10-3kg的固体放入注射器内;
Ⅱ.缓慢推动活塞至某一位置,记录活塞所在位置的容积刻度V及对应的气体压强P;
Ⅲ.重复步骤Ⅱ,记录几组P、V值;
Ⅳ.处理记录的数据,算出固体的密度.
(1)纵坐标取V,横坐标取
,请根据表格数据在方格图中(图2)画出相应图线;
(2)如果图线与纵坐标的截距为b,b表示的物理意义是
(3)该固体的密度为
Ⅰ.将质量为9.30×10-3kg的固体放入注射器内;
Ⅱ.缓慢推动活塞至某一位置,记录活塞所在位置的容积刻度V及对应的气体压强P;
Ⅲ.重复步骤Ⅱ,记录几组P、V值;
Ⅳ.处理记录的数据,算出固体的密度.
(1)纵坐标取V,横坐标取
| 1 |
| P |
(2)如果图线与纵坐标的截距为b,b表示的物理意义是
固体体积
固体体积
,写出图线对应的函数表达式:v=0.7
+0.265
| 1 |
| P |
v=0.7
+0.265
;| 1 |
| P |
(3)该固体的密度为
3.5×103
3.5×103
kg/m3.
| 测量次数 物理量 |
1 | 2 | 3 | 4 |
| P/105Pa | 0.77 | 1.00 | 1.33 | 1.82 |
| v/10-5m3 | 1.20 | 1.00 | 0.85 | 0.65 |

分析:(1)根据表格数据,描点作图即可
(2)注射器中的气体发生的是等温变化,根据玻意耳定律,PV=C,所以气体体积趋向于0时,P趋向于无穷大.从图象知,横轴截距表示固体的体积.再根据密度公式求出密度
(2)注射器中的气体发生的是等温变化,根据玻意耳定律,PV=C,所以气体体积趋向于0时,P趋向于无穷大.从图象知,横轴截距表示固体的体积.再根据密度公式求出密度
解答:解:(1)表格转换成1/P如下所示,然后描点作图如图2
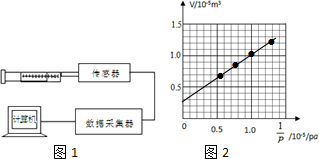
(2)根据根据玻意耳定律,PV=C,当
趋向于0,则,气体体积趋向于0,从V-
图象知,横轴截距表示固体的体积
由图象得 K=
=0.7 ①
K=
=0.7
解得;b=0.265 ②
v=0.7
+0.265 ③
(3)由(2)得,固体的体积 v=0.265m3
由ρ=
得:
固体的密度:ρ=
kg/m3=3.5×103kg/m3
答:(1)图象如上图所(2)固体的体积,v=0.7
+0.265 (3)3.5×103kg/m3


(2)根据根据玻意耳定律,PV=C,当
| 1 |
| P |
| 1 |
| P |
由图象得 K=
| 0.65-1.20 |
| 0.55-1.30 |
K=
| 0.65-b |
| 0.55-0 |
解得;b=0.265 ②
v=0.7
| 1 |
| P |
(3)由(2)得,固体的体积 v=0.265m3
由ρ=
| m |
| v |
固体的密度:ρ=
| 9.30×10-3 |
| 0.265×10-5 |
答:(1)图象如上图所(2)固体的体积,v=0.7
| 1 |
| P |
点评:解决本题的关键是掌握图象截距的含义,如在此图中,纵轴轴截距就表示固体的体积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012?长宁区二模)水平地面上有一个半径为R的圆形轨道,竖直平面上边中点P离地面高为h,P正下方一点P′位于COA连线上且与轨道圆心O的距离为L(L>R),如图所示.现从P点水平抛出质量为m的小沙袋,使其击中轨道上的小车(沙袋与小车均视为质点,空气阻力不计).求:
(2012?长宁区二模)水平地面上有一个半径为R的圆形轨道,竖直平面上边中点P离地面高为h,P正下方一点P′位于COA连线上且与轨道圆心O的距离为L(L>R),如图所示.现从P点水平抛出质量为m的小沙袋,使其击中轨道上的小车(沙袋与小车均视为质点,空气阻力不计).求: (2012?长宁区二模)如图所示的电路中,电源电动势为ε、内电阻为r (r小于外电路的总电阻),当滑动变阻器R的滑片P位于中点时,A、B、C三个灯泡均正常发光,且亮度相同,则( )
(2012?长宁区二模)如图所示的电路中,电源电动势为ε、内电阻为r (r小于外电路的总电阻),当滑动变阻器R的滑片P位于中点时,A、B、C三个灯泡均正常发光,且亮度相同,则( ) (2012?长宁区二模)如图1所示,圆形线圈P静止在水平桌面上,其正上方固定一螺线管Q,P和Q共轴,Q中通有按正弦函数规律变化的电流,其i-t图象如图2所示,P所受的重力为G,桌面对P的支持力为N,则( )
(2012?长宁区二模)如图1所示,圆形线圈P静止在水平桌面上,其正上方固定一螺线管Q,P和Q共轴,Q中通有按正弦函数规律变化的电流,其i-t图象如图2所示,P所受的重力为G,桌面对P的支持力为N,则( )