题目内容
19.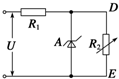 如图所示,A为一稳压管,它的作用是保证DE两端的电压UDE恒定不变,当流过稳压管的电流在20mA和80mA之间时,UDE就稳定在10V,R2为一可变电阻,它的最小值为500Ω,最大值为无穷大(即断路).设电源电压U=20V,则当R2变化时,为使UDE稳定在10V,R1可取下列几个电阻值中的( )
如图所示,A为一稳压管,它的作用是保证DE两端的电压UDE恒定不变,当流过稳压管的电流在20mA和80mA之间时,UDE就稳定在10V,R2为一可变电阻,它的最小值为500Ω,最大值为无穷大(即断路).设电源电压U=20V,则当R2变化时,为使UDE稳定在10V,R1可取下列几个电阻值中的( )| A. | 100Ω | B. | 200Ω | C. | 300Ω | D. | 4 000Ω |
分析 当R2无穷大时,流过R1的电流最小,为20mA;当R2取最小值时,电流最大,为80mA;结合UDE不变,根据欧姆定律求解.
解答 解:根据题意可知:U=20V,UDE=10V
所以有:U1=U-UDE=10V
当电阻R1取最大值时稳压管中的电流达到最小值20mA时,根据欧姆定律,得R1的电流最小值为:
I1max=0.02A+$\frac{{U}_{DE}}{{R}_{2}}$=0.02A+$\frac{10}{500}$A=0.04A
则有:R1=$\frac{{U}_{1}}{{I}_{max}}$=$\frac{10}{0.04}$=250Ω
当R1取最小值时稳压管中的电流达到最大值80mA时,R2的电阻为无穷大(即断路),根据欧姆定律,有:
R1min=$\frac{{U}_{1}}{{I}_{max}}$=$\frac{10}{0.08}$=125Ω
故R1的阻值范围为:125Ω<R1<250Ω,故B正确,ACD错误.
故选:B
点评 本题关键明确稳压管额工作原理,理清电路中的电流和电压关系,然后根据欧姆定律列式求解.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
10.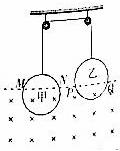 如图所示,两个完全相同的甲、乙金属圆环,用绝缘细线绕过光滑定滑轮相连并悬吊着,处于静止状态,圆环各有一部分处在方向水平的匀强磁场中,圆环与磁场的边界交点分别为M、N、P、Q,且MN=PQ<环的直径,若磁场发生一个微小变化,两环受到的安培力均小于环的重力,则下列说法正确的是( )
如图所示,两个完全相同的甲、乙金属圆环,用绝缘细线绕过光滑定滑轮相连并悬吊着,处于静止状态,圆环各有一部分处在方向水平的匀强磁场中,圆环与磁场的边界交点分别为M、N、P、Q,且MN=PQ<环的直径,若磁场发生一个微小变化,两环受到的安培力均小于环的重力,则下列说法正确的是( )
 如图所示,两个完全相同的甲、乙金属圆环,用绝缘细线绕过光滑定滑轮相连并悬吊着,处于静止状态,圆环各有一部分处在方向水平的匀强磁场中,圆环与磁场的边界交点分别为M、N、P、Q,且MN=PQ<环的直径,若磁场发生一个微小变化,两环受到的安培力均小于环的重力,则下列说法正确的是( )
如图所示,两个完全相同的甲、乙金属圆环,用绝缘细线绕过光滑定滑轮相连并悬吊着,处于静止状态,圆环各有一部分处在方向水平的匀强磁场中,圆环与磁场的边界交点分别为M、N、P、Q,且MN=PQ<环的直径,若磁场发生一个微小变化,两环受到的安培力均小于环的重力,则下列说法正确的是( )| A. | 甲、乙两个环仍保持静止 | |
| B. | 甲环向下运动,乙环向上运动 | |
| C. | 甲环有收缩趋势,乙环有扩张趋势 | |
| D. | 甲环受到的安培力大于乙环受到的安培力 |
11. 如图所示,有一匝接在电容器C两端的圆形导线回路,垂直于回路平面以内存在着向里的匀强磁场B,已知圆的半径r=5cm,电容C=20μF,当磁场B以4×10-2T/s的变化率均匀增加时,则( )
如图所示,有一匝接在电容器C两端的圆形导线回路,垂直于回路平面以内存在着向里的匀强磁场B,已知圆的半径r=5cm,电容C=20μF,当磁场B以4×10-2T/s的变化率均匀增加时,则( )
 如图所示,有一匝接在电容器C两端的圆形导线回路,垂直于回路平面以内存在着向里的匀强磁场B,已知圆的半径r=5cm,电容C=20μF,当磁场B以4×10-2T/s的变化率均匀增加时,则( )
如图所示,有一匝接在电容器C两端的圆形导线回路,垂直于回路平面以内存在着向里的匀强磁场B,已知圆的半径r=5cm,电容C=20μF,当磁场B以4×10-2T/s的变化率均匀增加时,则( )| A. | 电容器a板带正电,电荷量为2π×10-9C | |
| B. | 电容器a板带负电,电荷量为2π×10-9C | |
| C. | 电容器b板带正电,电荷量为4π×10-9C | |
| D. | 电容器b板带负电,电荷量为4π×10-9C |
8.物体做匀减速直线运动,最初两个2s内的位移分别10m和6m.则下列说法正确的是( )
| A. | 物体的初速度大小为6 m/s | B. | 物体的加速度大小为2m/s2 | ||
| C. | 物体第4s内的位移大小为5m | D. | 物体第4s末的速度大小为1m/s |
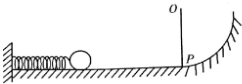 一个实验小组在“探究弹性势能的表达式”的实验中,利用了如图所示实验装置进行实验,光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O点转动的轻杆,且摆到某处就能停在该处,另有一小球,现在利用这些器材测定弹簧被压缩时的弹性势能.
一个实验小组在“探究弹性势能的表达式”的实验中,利用了如图所示实验装置进行实验,光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O点转动的轻杆,且摆到某处就能停在该处,另有一小球,现在利用这些器材测定弹簧被压缩时的弹性势能.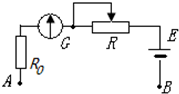 某同学想利用以下器材组装一只欧姆表,并比较精确地测量一只约几千欧电阻的阻值.
某同学想利用以下器材组装一只欧姆表,并比较精确地测量一只约几千欧电阻的阻值.