题目内容
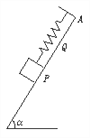
【题目】如图所示，在倾角α=60°的斜面上放一个质量m的物体，用k=100N/m的轻弹簧平行斜面吊着。发现物体放在PQ间任何位置都处于静止状态，测得AP=22cm，AQ=8cm，则物体与斜面间的最大静摩擦力等于多少？
【答案】Fm=7N
【解析】【试题分析】由题，当物体位于P点时，将要向上运动，静摩擦力沿斜面向下达到最大．当物体位于Q点时，物体将向下运动，静摩擦力沿斜面向上达到最大．根据平衡条件和胡克定律列方程求解最大静摩擦力．
设弹簧的原长为l0．
在P点有：k（Lap-l0）=mgsin60°+Fmax ①
在Q点有：k（Laq-l0）+Fmax=mgsin60° ②
联立①②得：kLap-kLaq=2Fmax
代入数值的Fmax=7N
练习册系列答案
相关题目
【题目】下表是某同学为探究弹力和弹簧伸长的关系所测的几组数据：
弹力F/N | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
弹簧的伸长量x/cm | 2.6 | 5.0 | 6.8 | 9.8 | 12.4 |
（1）请你在图中的坐标线上作出F-x图象.
（2）写出曲线所代表的函数.（x用m作单位）
（3）解释函数表达式中常数的物理意义.
