题目内容
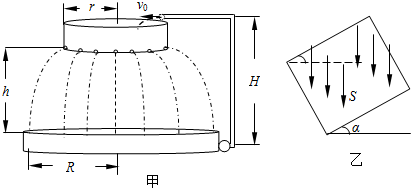
20. 如图所示,小球P固定于圆盘上,小球Q位于地面上,开始时小球P从圆盘的最低点绕圆盘的圆心做匀速圆周运动,同时小球Q以初速度v0=8m/s做竖直上抛运动,已知圆盘的圆心离地面的高h=2.4m,g=10m/s2,在运动过程中发现两小球在同一高度有速度相等的情况存在,问圆盘的半径是多大?
如图所示,小球P固定于圆盘上,小球Q位于地面上,开始时小球P从圆盘的最低点绕圆盘的圆心做匀速圆周运动,同时小球Q以初速度v0=8m/s做竖直上抛运动,已知圆盘的圆心离地面的高h=2.4m,g=10m/s2,在运动过程中发现两小球在同一高度有速度相等的情况存在,问圆盘的半径是多大?
分析 首先分析两球的运动情况,据两小球在同一高度有速度相等的情况存在,说明P球的运动方向竖直时才有可能速度相等;据Q此求出速度的大小和所需的时间;然后利用P的匀速圆周运动求半径.
解答 解:据两小球在同一高度有速度相等的情况存在,所以相遇的高度是与圆心等高处,且有两种可能,速度竖直向上和速度竖直向下两种可能.
据运动学公式${v}^{2}-{v}_{0}^{2}$=2as可知与圆心等高处的速度,v=$\sqrt{64-48}m/s$=4m/s ①
当速度方向竖直向上时相遇,据运动学速度公式v=v0+at得,t=$\frac{4-8}{-10}s$=0.4s
P的角速度为:ω=$\frac{2nπ+\frac{π}{2}}{0.4}$rad/s=5nπ+$\frac{5}{4}π$ (n=0、1、2、3,…) ②
又因为:v=ωr ③
联立①②③解得:r=$\frac{16}{20nπ+5π}$ m (n=0、1、2、3,…)
当速度方向竖直向下时相遇,据运动学速度公式v=v0+at得,t=$\frac{-4-8}{10}s$=1.2s
P的角速度为:ω=$\frac{2nπ+\frac{3π}{2}}{1.2}$rad/s=$\frac{5nπ}{3}+\frac{15π}{12}$ (n=0、1、2、3,…) ④
又因为:v=ωr ⑤
联立①④⑤解得:r=$\frac{48}{20nπ+15π}$ m (n=0、1、2、3,…)
答:圆盘的半径可能为$\frac{16}{20nπ+5π}$ m (n=0、1、2、3,…) 或$\frac{48}{20nπ+15π}$ m (n=0、1、2、3,…).
点评 此题的过程看似简单,实际较复杂,一定注意两小球在同一高度有速度相等的情况存在,据此求出速度和时间;一定注意圆周运动的周期性造成的多解.

| A. | 由a=$\frac{{v}^{2}}{r}$ 知,a与r成反比 | B. | 由ω=2πn 知,ω与转速n成正比 | ||
| C. | 由ω=$\frac{v}{r}$ 知,ω与r成反比 | D. | 由a=ω2r 知,a与r成正比 |
| A. | 垒球落地时瞬时速度的大小仅由初速度决定 | |
| B. | 垒球落地时瞬时速度的方向仅由击球点离地面的高度决定 | |
| C. | 垒球在空中运动的水平位移由初速度和高度共同决定 | |
| D. | 垒球在空中运动的时间仅由击球点离地面的高度决定 |
 质量m=0.1kg的小球套在轻杆上,杆固定在墙上;劲度系数为k=200N/m弹簧的一段固定在墙壁上,另一端与小球相连,当轻杆和水平面的夹角是37°时,小球恰好处于静止状态,此时弹簧的形变量为0.01m.小球和杆的动摩擦因数可能为( )
质量m=0.1kg的小球套在轻杆上,杆固定在墙上;劲度系数为k=200N/m弹簧的一段固定在墙壁上,另一端与小球相连,当轻杆和水平面的夹角是37°时,小球恰好处于静止状态,此时弹簧的形变量为0.01m.小球和杆的动摩擦因数可能为( )| A. | 0.25 | B. | 0.4 | C. | 0.5 | D. | 0.75 |
 如图所示,极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道,地球看作均匀球体).若已知一颗极地卫星从北纬300的正上方,按图示方向第一次运行至赤道正上方时所用的时间为0.25h,则同步卫星的线速度v1和该极地卫星的线速度v2大小之比为( )
如图所示,极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道,地球看作均匀球体).若已知一颗极地卫星从北纬300的正上方,按图示方向第一次运行至赤道正上方时所用的时间为0.25h,则同步卫星的线速度v1和该极地卫星的线速度v2大小之比为( )| A. | $\frac{1}{\sqrt{2}}$ | B. | $\frac{\sqrt{2}}{1}$ | C. | $\frac{1}{2}$ | D. | 2 |

 半圆形光滑轨道半径为R,固定在水平地面上,并使其轨道平面与地面垂直,如图所示,物体m1、m2同时由轨道左、右最高点释放,二者碰后粘在一起向上运动,求它们能上升的最大高度?
半圆形光滑轨道半径为R,固定在水平地面上,并使其轨道平面与地面垂直,如图所示,物体m1、m2同时由轨道左、右最高点释放,二者碰后粘在一起向上运动,求它们能上升的最大高度?