Question

（2011?娄底模拟）一辆客车在某高速公路上行驶，在经过某直线路段时，司机驾车做匀速直线运动．司机发现其正要通过正前方高山悬崖下的隧道，于是鸣笛，经时间t₁后听到回声；听到回声再行驶△t时间后，司机第二次鸣笛，又经时间t₂ 后，听到回声．已知声音在空中的传播速度为v₀．
（1）请根据以上条件推导客车速度的表达式．
（2）若此高速公路的最高限速为v_m=120km/h，声音在空中的传播速度为v₀=340m/s，测得t₁=6.6s，t₂=3.4s，△t=12s，请判断此客车是否超速．

Answer 1

分析：（1）根据题意可以求出声波前后两次从汽车到隧道所用的时间，结合声速，进而可以求出前后两次汽车到隧道之间的距离．由于汽车向着隧道方向运动，所以两者之间的距离在减小．汽车前后两次到隧道之间的距离之差即为汽车前进的路程．由于两次声波发出的时间间隔为△t．汽车运动的时间为从第一次与声波相遇开始，到第二次与声波相遇结束．求出这个时间，就是汽车运动的时间．根据汽车运动的距离和时间，即可求出汽车的运动速度表达式；
（2）此高速公路的最高限速为v_m=120km/h，声音在空中的传播速度为v₀=340m/s，测得t₁=6.6s，t₂=3.4s，△t=12s，将此代入第（1）可判定是否超速．

解答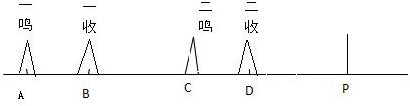：解：（1）依题可画出如图的运动示意图，由图可知
声波在时间t₁内路程为   
X_AP+X_BP=v₀t₁    
而车在时间t₁内路程为  X_AB=vt₁
声波在时间t₂内路程为   X_CP+X_DP=v₀t₂    而车在时间t₁内路程为  X_CD=vt₂
又车在△t内从B运动到C的过程有   X_BC=v△t
由几何关系得：X_BC=X_BP-X_CP    
 X_AP+X_BP=X_AB+2X_BP     
 X_cP+X_DP=2X_CP-X_CD
联立得 v=

v0(t1-t2)

2△t+t1+t2

（2）带入数值可求得  V=32m/s=115.2km/h＜120km/h
所以客车没有超速．
答：（1）客车速度的表达式为 v=

v0(t1-t2)

2△t+t1+t2

（2）客车没有超速．?

点评：如何确定汽车运动的时间，是此题的难点．两次信号的时间间隔虽然是12秒，但汽车在接收到两次信号时其通过的路程所对应的时间不是12秒．要从起第一次接收到超声波的信号开始计时，到第二次接收到超声波的信号结束，由此来确定其运动时间．通过的路程与通过这段路程所用的时间对应上是解决此题关键．