题目内容
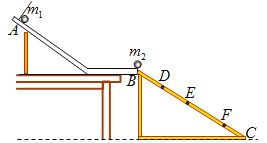
【题目】如图，两条足够长、间距为d的平行光滑金属直轨道MN、PQ与水平面成θ角，EF上方存在垂直导轨平面的如图乙所示的磁场，磁感应强度在0-T时间内按余弦规律变化（周期为T、最大值为B0），T时刻后稳定为B0．t=0时刻，正方形金属框ABCD在平行导轨向上的恒定外力作用下静止于导轨上。T时刻撤去外力，框将沿导轨下滑，金属框在CD边、AB边经过EF时的速度分别为v1和v2．已知金属框质量为m、边长为d、每条边电阻为R，框中磁场按余弦规律变化时产生的正弦式交变电流的峰值
，求：
（1）CD边刚过EF时，A、B两点间的电势差；
（2）撤去外力到AB边经过EF的总时间；
（3）从0时刻到AB边经过EF的过程中产生的焦耳热。
【答案】（1）
（2）
（3）
【解析】
（1）
、由楞次定律知A点电势低于B点，
故
、即 
（2）mgtsinθ-B0dq=mv2-mv0
故：
（3）交流电的有效值 
线框出磁场的过程中，
结合动能定理：
得：
总焦耳热为：
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
