题目内容
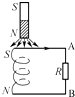
【题目】如图所示,有一斜面倾角为θ、质量为M的斜面体置于水平面山,A是最高点,B是最低点,C是AB的中点,其中AC段光滑、CB段粗糙.一质量为m的小滑块由A点静止释放,经过时间t滑至C点,又经过时间t到达B点.斜面体始终处于静止状态,取重力加速度为g,则( )

A. A到C与C到B过程中,滑块运动的加速度相同
B. A到C与C到B过程中,滑块运动的平均速度相等
C. C到B过程地面对斜面体的摩擦力水平向左
D. C到B过程地面对斜面体的支持力大于(M+m)g
【答案】BCD
【解析】根据牛顿第二定律得:AC段有:mgsinθ=ma1;BC段有:mgsinθ-μmgcosθ=ma2;可知,A到C与C到B过程中,滑块运动的加速度不同,故A错误.根据平均速度公式![]() 知,两个过程的位移和时间均相等,则平均速度相等.故B正确.设滑块到达C和B的速度分别为vC和vB.根据平均速度相等有:
知,两个过程的位移和时间均相等,则平均速度相等.故B正确.设滑块到达C和B的速度分别为vC和vB.根据平均速度相等有:![]() ,可得 vB=0,说明滑块由C到B过程做匀减速运动,加速度沿斜面向上,有水平向左的分加速度,对斜面和滑块整体,由牛顿第二定律知,地面对斜面体的摩擦力水平向左.故C正确.滑块由C到B过程做匀减速运动,加速度沿斜面向上,有竖直向上的分加速度,处于超重状态,所以地面对斜面体的支持力大于(M+m)g.故D正确.故选BCD.
,可得 vB=0,说明滑块由C到B过程做匀减速运动,加速度沿斜面向上,有水平向左的分加速度,对斜面和滑块整体,由牛顿第二定律知,地面对斜面体的摩擦力水平向左.故C正确.滑块由C到B过程做匀减速运动,加速度沿斜面向上,有竖直向上的分加速度,处于超重状态,所以地面对斜面体的支持力大于(M+m)g.故D正确.故选BCD.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目