题目内容
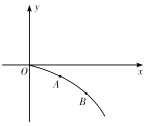
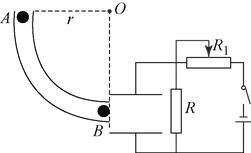
【题目】如图所示，绝缘光滑、内径很小的四分之一段而弧形管固定在整直平面内，圆弧半径
．一个直经略小于细圆管内径的带电小球质量
、电量
，从与
点等高的
点沿圆弧形管由静止运动到最低
，然后从点进入平行板电容器，刚好能沿水平方向做匀速直线运动．已知板间距离
，板长
，电源的电动势为
，内阻
，定值电阻
，取
．求：
（
）小球到达点时的速度；
（
）小球在板间做匀速直线运动时，电源的输出功率；
（
）若事先把滑动变阻器的阻值调到
，小球飞出极板时的偏移量为多少？
【答案】（
）
；（
）
；（
）
【解析】试题分析：（1）从A到B过程，应用动能定理可以求出小球的速度．（2）由平衡条件求出极板间的电压，然后应用欧姆定律求出电流，由电功率公式求出电源的输出功率．（3）应用欧姆定律求出两极板间的电压，小球在极板间做类平抛运动，应用类平抛运动规律可以求出偏移量．
（1）设小球到达B点时的速度为
，由动能定理得：
代入数据解得：
（2）小球在极板间做匀速直线运动，由平衡条件可得：
代入数据解得：
又电压
代入数据解得：电流
电源的输出功率：
代入数据解得：
（3）设将滑动变阻器的阻值调到
，回路中的电流为
则有：
代入数据解得：
两极板之间的电势差为：
代入数据解得：
设小球在两极间运动时的加速度为a，运动的时间为t，偏移量为y
则有：
，
，
联立解得：
练习册系列答案
相关题目
