题目内容
在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5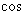 (kx+2
(kx+2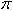 /3)单位米,式中K=1m-1。将一光滑小环套在该金属杆上,并从x=0处以v0=5m/s的初速度沿杆向下运动,取g=10m/s2,则 (1)当小环运动到x=
/3)单位米,式中K=1m-1。将一光滑小环套在该金属杆上,并从x=0处以v0=5m/s的初速度沿杆向下运动,取g=10m/s2,则 (1)当小环运动到x=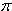 /3米时的速度大小为多少? (2)该小环在x轴方向能达到的最远距离是多少?
/3米时的速度大小为多少? (2)该小环在x轴方向能达到的最远距离是多少?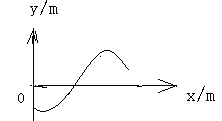
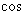 (kx+2
(kx+2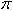 /3)单位米,式中K=1m-1。将一光滑小环套在该金属杆上,并从x=0处以v0=5m/s的初速度沿杆向下运动,取g=10m/s2,则 (1)当小环运动到x=
/3)单位米,式中K=1m-1。将一光滑小环套在该金属杆上,并从x=0处以v0=5m/s的初速度沿杆向下运动,取g=10m/s2,则 (1)当小环运动到x=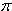 /3米时的速度大小为多少? (2)该小环在x轴方向能达到的最远距离是多少?
/3米时的速度大小为多少? (2)该小环在x轴方向能达到的最远距离是多少?
x=2.62m
试题分析:(1)解:x=0时, y1=-1.25m x=
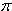 /3时,y2=-2.5m (2分)
/3时,y2=-2.5m (2分) 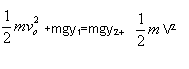
以y=0为零势能参考平面,由机械能守恒定律
解得:v=7.1m/s (4分)
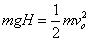
(2)小环在x轴最远处时,v=0 由机械能守恒定律
解得:H=1.25m。所以小环从y1=-1.25m处升至y3=0处即
2.5
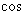 (kx+2
(kx+2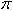 /3)=0 故:kx+2
/3)=0 故:kx+2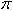 /3=n
/3=n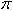 +
+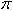 /2
/2取n=1,得:x=2.62m (9分)
点评:本题和数学的上的方程结合起来,根据方程来确定物体的位置,从而利用机械能守恒来解题,题目新颖,是个好题.

练习册系列答案
相关题目
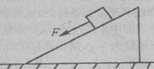



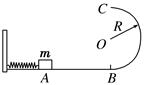
 ,仍要使物体恰能完成BC导轨上的圆周运动,则弹簧开始时的弹性势能至少为多少。
,仍要使物体恰能完成BC导轨上的圆周运动,则弹簧开始时的弹性势能至少为多少。