题目内容
17. 如图所示,质量m=1kg的长木板A放在水平地面上,在木板的最右端放一质量也为m=l kg的物块B.木板与地面间的动摩擦因数μ1=0.2,物块与木板间的动摩擦因数μ2=0.1.现用一水平力F=9N作用在木板上,使木板由静止开始匀加速运动,经过t1=1s,撤去拉力.最终物块没有滑离木板.设物块与木板间的最大静摩擦力等于滑动摩擦力.(g取10m/s2)求:
如图所示,质量m=1kg的长木板A放在水平地面上,在木板的最右端放一质量也为m=l kg的物块B.木板与地面间的动摩擦因数μ1=0.2,物块与木板间的动摩擦因数μ2=0.1.现用一水平力F=9N作用在木板上,使木板由静止开始匀加速运动,经过t1=1s,撤去拉力.最终物块没有滑离木板.设物块与木板间的最大静摩擦力等于滑动摩擦力.(g取10m/s2)求:(1)撤去拉力时,木板的速度大小v1.
(2)木板的最小长度L.
(3)物块最终与木板右端的距离s.
分析 (1)对木板进行受力分析,由牛顿第二定律求出加速度,然后由速度公式即可求出速度;
(2)求出物块的加速度与位移,然后求出木板减速的加速度,在求出二者速度相等时的速度,最后求出木板的长度;
(3)分别求出它们的位移即可求出物块最终与木板右端的距离s.
解答 解:(1)以木板为研究对象,竖直方向:mg+mg=FN
水平方向:F-μ1FN-μ2mg=ma1
代入数据得:${a}_{1}=4m/{s}^{2}$
所以,撤去拉力时,木板的速度大小:v1=a1t1=4×1=4m/s
(2)1s内木板的位移:${x}_{1}=\frac{1}{2}{a}_{1}{t}_{1}^{2}=\frac{1}{2}×4×{1}^{2}=2$m
以物块为研究对象,水平方向:ma2=μ2g
所以:${a}_{2}={μ}_{2}g=0.1×10=1m/{s}^{2}$
1s内物块的位移:${x}_{2}=\frac{1}{2}{a}_{2}{t}_{1}^{2}=\frac{1}{2}×1×{1}^{2}=0.5$m
撤去拉力后物块将继续加速一段时间,而木板做减速运动,设加速度为a3,则:
-μ2mg-μ1•2mg=ma3
代入数据得:${a}_{3}=-5m/{s}^{2}$
设再经过t2时间二者的速度相等,则:
v1+a3t2=a2(t1+t2)
代入数据得:t2=0.5s
t2时间内二者的位移:${x}_{1}′={v}_{1}{t}_{2}+\frac{1}{2}{a}_{3}{t}_{2}^{2}$
${x}_{2}′=\frac{1}{2}{a}_{2}({t}_{1}+{t}_{2})^{2}-\frac{1}{2}{a}_{2}{t}_{1}^{2}$
木板的长度至少为:L=x1+x1′-x2-x2′
代入数据得:L=2.25m
(3)达到相等的速度为:v′=a2(t1+t2)=1×(1+0.5)=1.5m/s
达到相等的速度后,物块和木板都做减速运动,直到停止,物块的加速度小,相对于木板向右运动,则:
木板的加速度:-μ1•2mg+μ2mg=ma4
物块的加速度保持不变,则:${x}_{1}″=\frac{{v}^{2}}{2{a}_{4}}$,${x}_{2}″=\frac{{v}^{2}}{2{a}_{2}}$
由几何关系:L+x1″=x2″+s
联立得:s=1.5m
答:(1)撤去拉力时,木板的速度大小是4m/s.
(2)木板的最小长度L是2.25m.
(3)物块最终与木板右端的距离是1.5m.
点评 本题关键明确木块和木板的运动规律和受力特点,根据牛顿第二定律求解出加速度后根据运动学公式规律联立求解.

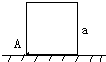 水平地面上竖直放一个边长为a的正方形薄板,其左下角顶点上有一点A,如图所示:现使该正方形在地面上不打滑地顺时针翻滚一周,则A点发生的位移大小和路程正确的是( )
水平地面上竖直放一个边长为a的正方形薄板,其左下角顶点上有一点A,如图所示:现使该正方形在地面上不打滑地顺时针翻滚一周,则A点发生的位移大小和路程正确的是( )| A. | 4a、$(1+\frac{{\sqrt{2}}}{2})πa$ | B. | 3a、$(1+\frac{{\sqrt{2}}}{2})πa$ | C. | 4a、$\frac{3}{2}πa$ | D. | 3a、$\frac{3}{2}πa$ |
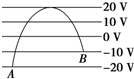 如图中的平行直线表示一簇垂直于纸面的等势面.一个电量为-5.0×10-8 C的粒子,沿图中曲线从A点移到B点,则下列说法正确的是( )
如图中的平行直线表示一簇垂直于纸面的等势面.一个电量为-5.0×10-8 C的粒子,沿图中曲线从A点移到B点,则下列说法正确的是( )| A. | 电场力做正功 | |
| B. | 粒子在B点的电势能一定小于在A点的电势能 | |
| C. | 粒子在B点的速度一定大于在A点的速度 | |
| D. | 粒子在A点和B点的速度大小一定相等 |

| A. | a点场强和c点场强相同 | |
| B. | c点场强大于b点场强 | |
| C. | 若将一检验电荷+q由a点移至b点,它受到的电场力增大 | |
| D. | 若将一电子放在d点,它受到的电场力方向沿着d点的电场方向 |
 如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点,仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点,仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,a的电势最低 | |
| B. | 带电质点在P点具有的电势能比在Q点具有的电势能大 | |
| C. | 带电质点通过P点时的动能比通过Q点时大 | |
| D. | 带电质点通过P点时的加速度比通过Q点时大 |
| 挂在橡皮绳下端的钩码个数 | 橡皮绳下端的坐标(xi/mm) | |
| 甲 | 乙 | |
| 1 | 216.5 | 216.5 |
| 2 | 246.7 | 232 |
| 3 | 284.0 | 246.5 |
| 4 | 335.0 | 264.2 |
| 5 | 394.5 | 281.3 |
| 6 | 462.0 | 301.0 |
(2)乙 同学的数据更符合实验要求(填“甲”或“乙”);
(3)为了更好地测量劲度系数,在选用钩码时需考虑的因素有哪些?尽可能使伸长量在弹性范围内,同时有足够大的伸长量,以减小长度测量的误差.
 如图所示,有一重力不计带正电的粒子q由M点进入一个负点电荷Q的电场中,虚线MN是粒子运动的轨迹,实线EF是一条电场线,下列说法正确的是( )
如图所示,有一重力不计带正电的粒子q由M点进入一个负点电荷Q的电场中,虚线MN是粒子运动的轨迹,实线EF是一条电场线,下列说法正确的是( )| A. | M点的电场强度大于N点的电场强度 | |
| B. | M点的电势高于N点的电势 | |
| C. | 粒子在M点的动能等于在N点的动能 | |
| D. | 料子在M点的电势能小于在N点的电势能 |
