题目内容
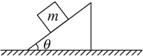
 如图,质量为m的小木块放在质量M、倾角为θ的光滑斜面上,斜面在水平推力F作用下,在光滑水平面上运动,木块与斜面保持相对静止,斜面对木块的支持力是( )
如图,质量为m的小木块放在质量M、倾角为θ的光滑斜面上,斜面在水平推力F作用下,在光滑水平面上运动,木块与斜面保持相对静止,斜面对木块的支持力是( )分析:斜面M、物体m在水平推力作用下一起加速,由牛顿第二定律可求出它们的加速度;然后结合质量可算出物体m的合力;最后利用物体的重力与合力可求出支持力.
解答:解:对(M+m)进行受力分析,如图所示

则由牛顿第二定律可知:F=(M+m)a
得 a=
(1)
对m进行受力分析,如图所示
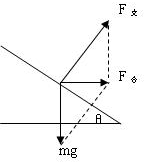
则有重力与支持力的合力是水平方向,所以用平行四边形定则将两力合成.
由三角函数关系可得:F支=
或者F支=
=
=
,
故A、C正确
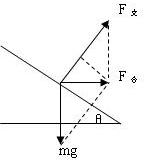
作一条垂直于支持力的直线,则有
F支=mgcosθ+F合sinθ=mgcosθ+
sinθ
因此D正确
故选ACD

则由牛顿第二定律可知:F=(M+m)a
得 a=
| F |
| (M+m) |
对m进行受力分析,如图所示

则有重力与支持力的合力是水平方向,所以用平行四边形定则将两力合成.
由三角函数关系可得:F支=
| mg |
| cosθ |
或者F支=
| F合 |
| sinθ |
| ma |
| sinθ |
| mF |
| (M+m)sinθ |
故A、C正确

作一条垂直于支持力的直线,则有
F支=mgcosθ+F合sinθ=mgcosθ+
| mF |
| (M+m) |
因此D正确
故选ACD
点评:从整体与隔离两角度对研究对象进行受力分析,同时掌握运用牛顿第二定律解题方法.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
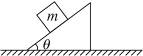
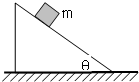 如图所示,一个倾角为θ的木楔固定在水平地面上,在其斜面上放有一个质量为m的小物块,整个装置处于静止状态.那么,在某段时间t内木楔的斜面对小物块的冲量的大小和方向是( )
如图所示,一个倾角为θ的木楔固定在水平地面上,在其斜面上放有一个质量为m的小物块,整个装置处于静止状态.那么,在某段时间t内木楔的斜面对小物块的冲量的大小和方向是( )