题目内容
【题目】如图甲所示,x轴正方向水平向右,y轴正方向竖直向上.在xOy平面内有与y轴平行的匀强电场,在半径为R的圆形区域内加有与xOy平面垂直的匀强磁场.在坐标原点O处放置一带电微粒发射装置,它可以连续不断地发射具有相同质量m、电荷量q(q>0)和初速度为v0的带电微粒.(已知重力加速度为g)
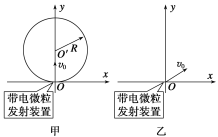
(1)当带电微粒发射装置连续不断地沿y轴正方向发射这种带电微粒时,这些带电微粒将沿圆形磁场区域的水平直径方向离开磁场,并继续沿x轴正方向运动.求电场强度E和磁感应强度B的大小和方向.
(2)调节坐标原点处的带电微粒发射装置,使其在xOy平面内不断地以相同速率v0沿不同方向将这种带电微粒射入第Ⅰ象限,如图乙所示.现要求这些带电微粒最终都能平行于x轴正方向运动,则在保证电场强度E和磁感应强度B的大小和方向不变的条件下,求出符合条件的磁场区域的最小面积.
【答案】(1)E=![]() ,沿y轴正方向 B=
,沿y轴正方向 B=![]() ,垂直纸面向外 (2)(
,垂直纸面向外 (2)(![]() -1)R2
-1)R2
【解析】
试题分析: (1)微粒沿x轴正方向运动,即带电微粒所受重力与电场力平衡.
设电场强度大小为E,由平衡条件得:mg=qE
解得:E=![]()
由于粒子带正电,故电场方向沿y轴正方向
带电微粒进入磁场后,做匀速圆周运动,且半径r=R.
设匀强磁场的磁感应强度大小为B.
由牛顿第二定律得:qv0B=m![]()
解得B=![]() ,磁场方向垂直纸面向外.
,磁场方向垂直纸面向外.
(2)沿y轴正方向射入的微粒,运动轨迹如图所示:
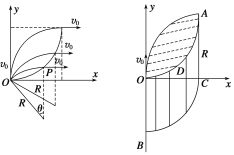
以半径R沿x轴正方向运动四分之一圆弧,该圆弧也恰为微粒运动的上边界.以O点为圆心、R为半径做的四分之一圆弧BC为微粒做圆周运动的圆心轨迹.微粒经磁场偏转后沿x轴正方向运动,即半径沿竖直方向.并且射出点距圆心轨迹上各点的距离为R,射出点的边界与圆弧BC平行,如图中的圆弧ODA,圆弧OA与圆弧ODA之间的区域即为磁场区域的最小面积:
S=2(![]() πR2-
πR2-![]() R2)=(
R2)=(![]() -1)R2.
-1)R2.