题目内容
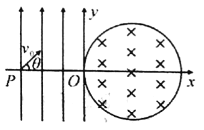
【题目】如图所示质量为m的物块A在光滑的水平面上以一定的速度向右滑行，质量为2m的圆弧体静止在光滑水平面上，光滑圆弧面最低点与水平面相切，圆弧的半径为R，圆弧所对的圆心角θ=53°，物块滑上圆弧体后，刚好能滑到圆弧体的最高点，重力加速度为g。求
(1)物块在水平面上滑行的速度大小；
(2)若将圆弧体锁定，物块仍以原来的速度向右滑行并滑上圆弧体，则物块从圆弧面上滑出后上升到最高点的速度大小及最高点离地面的高度。
【答案】（1）
（2）
【解析】
（1）A、B组成的系统在水平方向动量守恒，应用动量守恒定律与机械能守恒定律可以求出物块A的速度。
（2）圆弧体固定，物块上滑过程机械能守恒，应用机械能守恒定律可以求出到达圆弧体上端时的速度，离开圆弧体后物块做斜上抛运动，应用运动的合成与分解可以求出到达最高点的速度，应用机械能守恒定律可以求出上升的最大高度。
（1）物块与圆弧体组成的系统在水平方向动量守恒，物块到达最高点时两者速度相等，以向右为正方向，由动量守恒定律得：mv0=（m+2m）v，
由机械能守恒定律得：
mv02＝(m+2m)v2+mgR(1cosθ)，
解得：；
（2）对物块，由机械能守恒定律得：mv02＝mv12+mgR(1cosθ)，
解得： 
；
物块从圆弧最高点抛出后，在水平方向做匀速直线运动，竖直方向做竖直上抛运动，
物块到达最高点时，物块的速度：v2=v1cosθ=
，
由机械能守恒定律得：mv02=mgh+mv22，
解得：h=
R；
练习册系列答案
相关题目
