题目内容
16.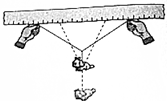 如图所示,在一根长度已知的细线中央悬挂一件重力已知的重物,然后沿着直尺将双手慢慢分开,观察分开到什么距离时细线断了,这样就可以计算出细线能承受的最大拉力.请说出计算的依据,并列出计算公式.
如图所示,在一根长度已知的细线中央悬挂一件重力已知的重物,然后沿着直尺将双手慢慢分开,观察分开到什么距离时细线断了,这样就可以计算出细线能承受的最大拉力.请说出计算的依据,并列出计算公式.
分析 把一重为G的物体系在绳的中点,将绳子左右对称分开,即两个力的合力不变且夹角在逐渐变大,故两个力逐渐变大,读出绳子断裂时绳子端点的距离,根据平衡条件列式求解.
解答 解:设细线的长度为l,受力分析如图: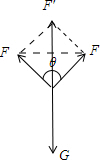
两个力的合力不变始终等于G,且夹角在逐渐变大,故两个力逐渐变大,当绳子端点的距离为x时,绳子断裂,两侧绳子的拉力达到最大,
则由这两侧的力在竖直方向的分量之和等于重力G得:
2Fcos$\frac{θ}{2}$=G
根据几何关系,cos$\frac{θ}{2}=\frac{\sqrt{{l}^{2}-{x}^{2}}}{l}$,
解得:F=$\frac{Gl}{2\sqrt{{l}^{2}-{x}^{2}}}$
答:当绳子端点的距离为x时,绳子断裂,两侧绳子的拉力达到最大,根据平衡条件即可求出最大承受拉力,计算公式为F=$\frac{Gl}{2\sqrt{{l}^{2}-{x}^{2}}}$.
点评 对结点进行受力分析,找到临界条件,应用受力平衡列式求解即可.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
7.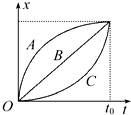 A、B、C三质点同时同地沿一直线运动,其x-t图象如图所示,则在0~t0这段时间内,下列说法中正确的是( )
A、B、C三质点同时同地沿一直线运动,其x-t图象如图所示,则在0~t0这段时间内,下列说法中正确的是( )
 A、B、C三质点同时同地沿一直线运动,其x-t图象如图所示,则在0~t0这段时间内,下列说法中正确的是( )
A、B、C三质点同时同地沿一直线运动,其x-t图象如图所示,则在0~t0这段时间内,下列说法中正确的是( )| A. | 质点A的位移最大 | B. | 质点C的平均速度最小 | ||
| C. | B质点做匀速直线运动 | D. | 三质点平均速度一定不相等 |
8.如图甲、乙所示为某物体在0~t时间内运动的x-t图线和v-t图线,由图可知,在0~t时间内( )
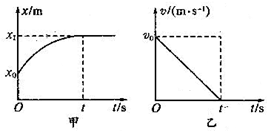

| A. | 物体做的是曲线运动 | B. | 物体做加速度越来越小的运动 | ||
| C. | 甲图中$\frac{t}{2}$时刻,图线的斜率为$\frac{{v}_{0}}{2}$ | D. | x1-x0>$\frac{{v}_{0}}{2}$t |
13. 在水平地面上放一质量为1.0kg木块,木块与地面间的动摩擦因数为0.6,在水平方向对木块同时施加相互垂直的两个力F1、F2,如图所示,已知F1=3.0N,F2=4.0N,g取10N/kg,(假设最大静摩擦力等于滑动摩擦力)则( )
在水平地面上放一质量为1.0kg木块,木块与地面间的动摩擦因数为0.6,在水平方向对木块同时施加相互垂直的两个力F1、F2,如图所示,已知F1=3.0N,F2=4.0N,g取10N/kg,(假设最大静摩擦力等于滑动摩擦力)则( )
 在水平地面上放一质量为1.0kg木块,木块与地面间的动摩擦因数为0.6,在水平方向对木块同时施加相互垂直的两个力F1、F2,如图所示,已知F1=3.0N,F2=4.0N,g取10N/kg,(假设最大静摩擦力等于滑动摩擦力)则( )
在水平地面上放一质量为1.0kg木块,木块与地面间的动摩擦因数为0.6,在水平方向对木块同时施加相互垂直的两个力F1、F2,如图所示,已知F1=3.0N,F2=4.0N,g取10N/kg,(假设最大静摩擦力等于滑动摩擦力)则( )| A. | 木块受到的摩擦力大小为6N | |
| B. | 木块受到的摩擦力大小为5N | |
| C. | 木块在水平方向受到的合力大小为1N | |
| D. | 若F1顺时针转90°,此时木块在水平方向受到的合力大小为0 |
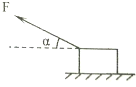 重为G的物体放在水平面上,与地面间动摩擦因数为μ,用与水平方向成α角的力F拉物体,如图所示,使它做匀速运动,则力F的大小为多少?
重为G的物体放在水平面上,与地面间动摩擦因数为μ,用与水平方向成α角的力F拉物体,如图所示,使它做匀速运动,则力F的大小为多少?