��Ŀ����
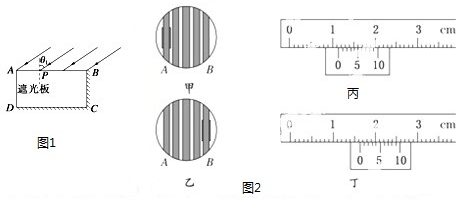
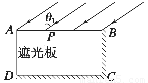
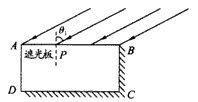
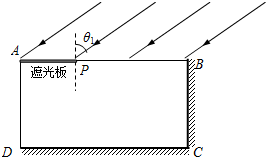 ʵ������һ������������ɵij����壬��ͼ��ABCD��ʾ��AB�ij���Ϊl1��AD�ij���Ϊl2����AB��AD���⣬��BC��CD�߲��⣨�䵽�������ߵĹ��߾���ȫ�����գ�������һƽ�й���������Ǧ�1�䵽AB�棬������� AD�����й��������������ͬѧ�ֱ��ò�ͬ�ķ��������ó�������ʵ������ʣ�
ʵ������һ������������ɵij����壬��ͼ��ABCD��ʾ��AB�ij���Ϊl1��AD�ij���Ϊl2����AB��AD���⣬��BC��CD�߲��⣨�䵽�������ߵĹ��߾���ȫ�����գ�������һƽ�й���������Ǧ�1�䵽AB�棬������� AD�����й��������������ͬѧ�ֱ��ò�ͬ�ķ��������ó�������ʵ������ʣ���1����ͬѧ�������ǣ������䵽AB���Ϲ��ߵ�����Dz��䣬��һ�ڹ����A����AB�����ƽ����ڹ��ǰ���Ƶ�Pʱ��AD����ǡ��������������AP�ij���Ϊl3��������ʵ������ʿɱ�ʾΪn=
��2����ͬѧ�������ǣ����������䵽AB���Ϲ��ߵ�����ǣ�ʹAD��Ҳǡ�������������ô�ʱ�䵽AB���Ϲ��ߵ������Ϊ��2��������ʵ������ʿɱ�ʾΪn=
��3����1�ͦ�2�Ĺ�ϵΪ����1
��������1�����ݼ���֪ʶ��������r1���������䶨����������ʣ�
��2����AD���Ϸ���ȫ���䣬˵����AD���ϵ�����ǵ����ٽ��C�������ٽ�ǹ�ʽsinC=
�����䶨�ɽ����������ʣ�
��3���ɼ��ι�ϵ����������AD���ϵ��������AB���ϵ�����ǵĹ�ϵ��������AD���ϵ������Խ��Խ������ȫ���䣬������1����2�Ĵ�С��
��2����AD���Ϸ���ȫ���䣬˵����AD���ϵ�����ǵ����ٽ��C�������ٽ�ǹ�ʽsinC=
| 1 |
| n |
��3���ɼ��ι�ϵ����������AD���ϵ��������AB���ϵ�����ǵĹ�ϵ��������AD���ϵ������Խ��Խ������ȫ���䣬������1����2�Ĵ�С��
���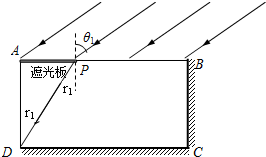 �⣺��1���������Ϊr1���ڡ�APD�У��ɼ��ι�ϵ�ã�
�⣺��1���������Ϊr1���ڡ�APD�У��ɼ��ι�ϵ�ã�
sinr1=
������AB���Ϸ������䣬�����䶨�ɿɵý��ʵ�������Ϊ��n=
=
��
��2���䵽AB���ϵĹ��ߵ������Ϊ��2ʱ����AD���Ϸ���ȫ���䣬˵����AD���ϵ�����ǵ����ٽ�ǣ�
����AB���ϵ������Ϊr2�������䶨�ɵã�
=n ��
���ٽ�Ǽ��㹫ʽ�ã�sinC=
���ɼ��ι�ϵ�ɵã�r2+C=90�㣬
sinr2=sin��90��-C��=cosC=
=
��
�ɢ٢�������ã�n=
��
��3������AB���ϵ������Ϊr���ɼ��ι�ϵ��֪��AD���ϵ������Ϊ��i=90��-r����AB���ϵ������ԽС������AB���ϵ������ԽС������AD���ϵ������Խ��Խ������ȫ���䣬������1����2��
�ʴ�Ϊ����1��
����2��
����3������
 �⣺��1���������Ϊr1���ڡ�APD�У��ɼ��ι�ϵ�ã�
�⣺��1���������Ϊr1���ڡ�APD�У��ɼ��ι�ϵ�ã�sinr1=
| l3 | ||||||
|
| sin��1 |
| sinr1 |
| ||||||
| l3 |
��2���䵽AB���ϵĹ��ߵ������Ϊ��2ʱ����AD���Ϸ���ȫ���䣬˵����AD���ϵ�����ǵ����ٽ�ǣ�
����AB���ϵ������Ϊr2�������䶨�ɵã�
| sin��2 |
| sinr2 |
���ٽ�Ǽ��㹫ʽ�ã�sinC=
| 1 |
| n |
sinr2=sin��90��-C��=cosC=
| 1-sin2C |
1-
|
�ɢ٢�������ã�n=
| 1+sin2��2 |
��3������AB���ϵ������Ϊr���ɼ��ι�ϵ��֪��AD���ϵ������Ϊ��i=90��-r����AB���ϵ������ԽС������AB���ϵ������ԽС������AD���ϵ������Խ��Խ������ȫ���䣬������1����2��
�ʴ�Ϊ����1��
| ||||||
| l3 |
| 1+sin2��2 |
�������������ؼ�Ҫ��ȷ����ȫ�����������������ü���֪ʶ�������ǣ�

��ϰ��ϵ�д�
 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
�����Ŀ