题目内容
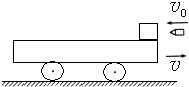
【题目】如图，在足够长的光滑水平面上，物体A、B、C位于同一直线上，A点位于B、C之间，A的质量为m，B、C的质量都为M，三者均处于静止状态，现使A以某一速度向右运动，求m和M之间应满足什么条件，才能使A只与B、C各发生一次碰撞．设物体间的碰撞都是弹性的．
【答案】解：A向右运动与C发生碰撞的过程中系统的动量守恒、机械能守恒，选取向右为正方向，设开始时A的速度为v0 ， 第一次与C碰撞后C的速度为vC1 ， A的速度为vA1 ． 由动量守恒定律、机械能守恒定律得：
mv0=mvA1+MvC1①
②
联立①②得： 
③ 
④
可知，只有m＜M时，A才能被反向弹回，才可能与B发生碰撞．
A与B碰撞后B的速度为vB1 ， A的速度为vA2 ． 由动量守恒定律、机械能守恒定律，同理可得： 
= 
⑤
根据题意要求A只与B、C各发生一次碰撞，应有：vA2≤vC1⑥
联立④⑤⑥得：m2+4mM﹣M2≥0
解得： 
，（另一解： 
舍去）所以m与M之间的关系应满足：
答：m和M之间应满足 ，才能使A只与B、C各发生一次碰撞
【解析】本题考查了水平方向的动量守恒定律问题，分析清楚物体运动过程、应用动量守恒定律、能量守恒定律即可正确解题．
【考点精析】认真审题，首先需要了解动量守恒定律(动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变)．
练习册系列答案
金钥匙试卷系列答案
相关题目
