题目内容
14.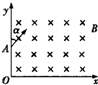 在直角坐标系xOy的第一象限内有垂直于纸面向里的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带负电粒子从y轴正半轴上的A点以与y轴正方向夹角为α=45°的速度垂直磁场方向射入磁场,如图所示,已知OA=a,不计粒子的重力,则下列说法正确的是( )
在直角坐标系xOy的第一象限内有垂直于纸面向里的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带负电粒子从y轴正半轴上的A点以与y轴正方向夹角为α=45°的速度垂直磁场方向射入磁场,如图所示,已知OA=a,不计粒子的重力,则下列说法正确的是( )| A. | 若粒子垂直于x轴离开磁场,则粒子进入磁场时的初速度大小为$\frac{\sqrt{2}qBa}{m}$ | |
| B. | 改变粒子的初速度大小,可以使得粒子刚好从坐标系的原点O离开磁场 | |
| C. | 粒子在磁场中运动的最长时间为$\frac{3πm}{2qB}$ | |
| D. | 从x轴射出磁场的粒子中,粒子的速度越大,在磁场中运动的时间就越短 |
分析 粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由几何知识求出粒子轨道半径与转过的圆心角,然后应用牛顿第二定律与周期公式分析答题.
解答 解:A、粒子垂直于x轴离开磁场,粒子运动轨迹如图所示:
由几何知识得:r=$\frac{a}{sin45°}$=$\sqrt{2}$a,
粒子在磁场中做圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,解得:v=$\frac{\sqrt{2}qBa}{m}$,故A正确;
B、粒子在磁场中做圆周运动,粒子速度较小时从y轴离开磁场,当粒子速度为某一值v时与x轴相切,此时粒子不过坐标原点,当速度大于v时,粒子从x轴离开磁场,如图所示,粒子不可能从坐标系的原点O离开磁场,故B错误;

C、粒子从y轴离开磁场时在磁场中转过的圆心角最大,运动时间最长,运动轨迹如图所示:
由几何知识可知,粒子转过的圆心角:θ=270°,粒子在磁场中的最长运动时间:t=$\frac{θ}{360°}$T=$\frac{270°}{360°}$×$\frac{2πm}{qB}$=$\frac{3πm}{2qB}$,故C正确;
D、从x轴射出磁场的粒子中,粒子的速度越大,粒子在磁场中转过的圆心角θ越小,在磁场中运动的时间:t=$\frac{θ}{2π}$T越小,故D正确;
故选:ACD.
点评 本题考查了粒子在磁场中的运动,分析清楚粒子运动过程、作出粒子运动轨迹是解题的关键,应用牛顿第二定律与粒子做圆周运动的周期公式可以解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列说法中不正确的是( )
| A. | 由磁感应强度的定义式B=$\frac{F}{IL}$可知,磁场中某处的磁感应强度大小与通电直导线所受磁场力成正比,与IL成反比 | |
| B. | 一小段通电直导线磁场中某处所受的磁场力的方向就是该处磁场的方向 | |
| C. | 一小段通电直导线放在某处受到的磁场力等于零,则该处磁感应强度一定为零 | |
| D. | 一段长为10cm、电流为2A的通电直导线在某处受磁场力大小为0.8N,则该处磁感应强度的大小至少为4T |
2.关于做自由落体运动的物体,下列说法正确的是( )
| A. | 第1s末、第2s末、第3s末的瞬时速度之比为1:2:3 | |
| B. | 前1s内、前2s内、前3s内下落高度之比为1:3:5 | |
| C. | 第1s、第2s、第3s下落的高度之比为1:4:9 | |
| D. | 第1s内、第2s内、第3s内的平均速度之比为1:2:3 |
 如图所示,小球在轻弹簧和水平轻绳的拉力作用下处于静止状态.弹簧与竖直方向的夹角θ=37°,弹簧的拉力F=10N,伸长量为x=0.01m,sin37°=0.6,cos37°=0.8.
如图所示,小球在轻弹簧和水平轻绳的拉力作用下处于静止状态.弹簧与竖直方向的夹角θ=37°,弹簧的拉力F=10N,伸长量为x=0.01m,sin37°=0.6,cos37°=0.8.
 如图所示,皮带传动中,O1、O2两轮的轴固定,当主动轮O1先逆时针转动时,不打滑的皮带也使从动轮O2逆时针转动,试确定两轮边缘上的A点和B点所受摩擦力的方向.
如图所示,皮带传动中,O1、O2两轮的轴固定,当主动轮O1先逆时针转动时,不打滑的皮带也使从动轮O2逆时针转动,试确定两轮边缘上的A点和B点所受摩擦力的方向.