题目内容
明理同学很注重锻炼身体，能提起50 kg的重物．现有一个倾角为15°的粗糙斜面，斜面上放有重物，重物与斜面间的动摩擦因数μ＝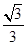
≈0.58，求他能沿斜面向上拉动重物质量的最大值．
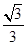≈0.58，求他能沿斜面向上拉动重物质量的最大值．70.7 kg
该同学能产生的最大拉力为F，由题意得F＝mg①
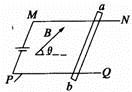
设该同学在斜面上拉动重物M的力F与斜面成φ角，重物受力如图所示．
由平衡条件知垂直斜面方向
FN＋Fsin φ－Mgcos φ＝0②
平行斜面方向
Fcos φ－μFN－Mgsin θ＝0③
联立②③式得M＝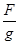
·
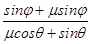④
令μ＝tan α⑤
联立④⑤式得，M＝·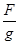
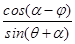⑥
要使质量最大，分子须取最大值，
即cos(α－φ)＝1，即α＝φ⑦
此时拉动的重物的质量的最大值为
Mmax＝·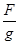
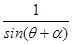.⑧
由题给数据tan α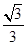＝，即α＝30°.⑨
联立⑦⑧⑨式代入数值解得，Mmax＝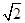
m＝70.7 kg.⑩
设该同学在斜面上拉动重物M的力F与斜面成φ角，重物受力如图所示．
由平衡条件知垂直斜面方向
FN＋Fsin φ－Mgcos φ＝0②
平行斜面方向
Fcos φ－μFN－Mgsin θ＝0③
联立②③式得M＝
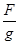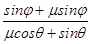·④令μ＝tan α⑤
联立④⑤式得，M＝
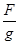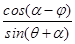·⑥要使质量最大，分子须取最大值，
即cos(α－φ)＝1，即α＝φ⑦
此时拉动的重物的质量的最大值为
Mmax＝
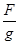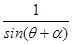·.⑧由题给数据tan α＝
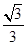，即α＝30°.⑨联立⑦⑧⑨式代入数值解得，Mmax＝
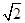m＝70.7 kg.⑩
练习册系列答案
相关题目
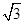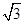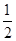mg ;mg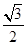 
；
mg
mg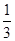
mg
mg