��Ŀ����
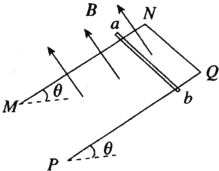
����Ŀ����ͼ��ʾ������Ϊm2��2.95kg�ij�ľ��B����ֹ�ڴֲڵ�ˮƽ�����ϣ�����Ϊm3��1.00kg�����C������Ϊ�ʵ㣩���ڳ�ľ������Ҷˡ�һ������Ϊm1��0.05kg���ӵ�A���ٶ�v0��360m/s���ų�ľ���˶����ӵ����볤ľ�岢�������У��ӵ����볤ľ���ʱ�伫�̣��������������Cʼ���ڳ�ľ���ϡ���֪��ľ��������Ķ�Ħ������Ϊ��1��0.20�����C�볤ľ���Ķ�Ħ��������2��0.40�����C�볤ľ�������Ħ�������ڻ���Ħ������gȡ10m/s2����
(1)�ӵ����볤ľ���˲�䳤ľ��B���ٶȣ�
(2)��ľ��B����С���ȡ�
![]()
���𰸡�(1)6m/s��(2)2.25m
��������
(1)��A��Bϵͳ���ɶ����غ㶨�ɵã�
m1v0��(m1��m2)v1
���
v1��6m/s
(2)֮��AB�������˶���C�����˶���BC�ﵽ��ͬ�ٶ�֮ǰ����ľ����ӵ���
��2m3g����1(m1��m2��m3)g��(m1��m2)a1
�����C
��2m3g��m3a2
�����ײ��ﵽ��ͬ�ٶȾ�����ʱ��Ϊt����
v1��a1t��a2t
�˹��������C���ľ��B��λ��Ϊ
d��v1t��![]() a1t2��
a1t2��![]() a2t2��2.25m
a2t2��2.25m
BC�ﵽ��ͬ�ٶ�֮������1<��2������һ�����ͣ�£��ʳ�ľ�����С����Ϊ2.25m

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ