��Ŀ����
11��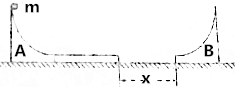 ��ͼ��ʾ��A��BΪ������ͬ��$\frac{1}{4}$�⻬Բ��������̶���ˮƽ���ϣ���Բ���뾶��ΪR=1.8m�����A�Ҳ�������ˮƽ���ϵij�ľ���������������ճ������ľ������M=2kg���ϱ�����Բ�����ĩ�����У��Ҷ˾�����B�����x=0.6m���ֽ�����Ϊm=1kg����飨����Ϊ�ʵ㣩�ӹ��A��ߵ������ͷţ����ϳ�ľ�������ľ�����һ�������Բ�����B�����������ճ����һ����֪С�����ľ���Ķ�Ħ������Ϊ��1=0.5��ľ����ˮƽ���Ķ�Ħ������Ϊ��2=0.1��gȡ10m/s2����
��ͼ��ʾ��A��BΪ������ͬ��$\frac{1}{4}$�⻬Բ��������̶���ˮƽ���ϣ���Բ���뾶��ΪR=1.8m�����A�Ҳ�������ˮƽ���ϵij�ľ���������������ճ������ľ������M=2kg���ϱ�����Բ�����ĩ�����У��Ҷ˾�����B�����x=0.6m���ֽ�����Ϊm=1kg����飨����Ϊ�ʵ㣩�ӹ��A��ߵ������ͷţ����ϳ�ľ�������ľ�����һ�������Բ�����B�����������ճ����һ����֪С�����ľ���Ķ�Ħ������Ϊ��1=0.5��ľ����ˮƽ���Ķ�Ħ������Ϊ��2=0.1��gȡ10m/s2������С���ͨ��Բ�����A����͵�ʱ�Թ����ѹ����
����С��鲻��ľ���ϻ��£�ľ���ܻ�õ�����ٶȣ�
����ʹС����ܹ�����Բ�����B��ľ�峤��Ӧ�����������
���� �ٶ���������ɻ�е���غ㶨�ɿ���õ���ײ����ٶȣ�������������ʽ�����֧������ ����ţ�ٵ������ɿ����ѹ����
�ڷ�����������˶����̣�֪�����岻��ľ���ϻ������ն��ߴ���ͬ�ٶ�ʱ�ٶȴ���� ����ţ�ٵڶ����ɿ���ü��ٶȣ������˶�ѧ��ʽ������ٶȣ�
����ȷ�����ľ����˶����̣��ֱ���������ľ��ľ��룬�Ӷ����ľ�����Сֵ���ٶԴﹲͬ�ٶ�֮��Ĺ��̷������ɶ��ܶ��������������ľ���ϻ��еľ��룻�����ö�Ӧ�����ֵ��
��� �⣺��1������������ɻ�е���غ㶨�ɿ�֪��
mgR=$\frac{1}{2}$mv2��
�������ݽ�ã�v=6m/s��
��A������������ʽ��֪��
F-mg=m$\frac{{v}^{2}}{R}$
������ã�F=30N��
��ţ�ٵ������ɿ�֪��֧����Ϊ30N��
��2��С��鲻��ľ���ϻ��£�����ͬ��ʱ��ľ��ﵽ����ٶȣ�
ľ���������˶�����ľ����ţ�ٵڶ����ɿ�֪��
��1mg=ma1��
�������ݽ�ã�a1=-5m/s2��
ľ�����ȼ���ֱ���˶�����ľ�������֪����1mg-��2��M+m��g=Ma
�������ݽ�ã�a2=1m/s2��
�������ٶ����ʱ��ľ�������ٶȣ����У�
v0t+a1t=a2t
��ã�t=1s��
��ʱľ���λ��Ϊ��x=$\frac{1}{2}$a2t2=$\frac{1}{2}$��1��1=0.5m��
˵��ľ�廹û�е�����B����˵������ٶ�Ϊ��v=a2t=1��1=1m/s��
��3��Ҫʹ����ܻ���B��������廬��B�����ʱ���ٶ�Ӧ���ڵ����㣻�ﵽ��Ծ�ֹʱ�������λ��Ϊ��
x1=v0t+$\frac{1}{2}$a1t2=6��1-$\frac{1}{2}��5��1$=3.5m��
����ʱľ���λ��Ϊ0.5m����ľ������Ӧ����3.5-0.5=3m��
�������Ծ�ֹ�����ǰ������ǰ��L=0.1m�Ĺ����У��ɶ��ܶ�����֪��
-��2��m+M��gL=$\frac{1}{2}$��m+M��v22-$\frac{1}{2}$��M+m��v2
�������ݽ�ã�v2=$\frac{2\sqrt{5}}{5}$m/s��
������������ǰ����Ҫʹ�ܻ���B����鵽��Bʱ���ٶ�Ӧ�����㣻 ���У�
-��1mgL1=0-$\frac{1}{2}$mv22
�������ݽ�ã�L1=0.8m��
��˵��ľ����ֵӦΪ��3+0.8=3.8m��
��Ҫʹ�����ܻ���B��ľ��ij���ӦΪ��3m��L��3.8m��
�𣺢�С���ͨ��Բ�����A����͵�ʱ�Թ����ѹ��Ϊ30N��
����С��鲻��ľ���ϻ��£�ľ���ܻ�õ�����ٶ�Ϊ1m��
����ʹС����ܹ�����Բ�����B��ľ�峤��Ӧ���������Ϊ��3m��L��3.8m��
���� ���⿼�鶯�ܶ�����ţ�ٵڶ����ɵ�Ӧ���Լ��˶�ѧ��ʽ��Ӧ�ã�Ҫע����ȷ�����������̣�ͬʱ�ֱ����������з�������ȷ�������ɵ�Ӧ�ò���ȷ��⣬��������̸��ӣ��������⣮

| A�� | $\frac{2��R}{T}$ | B�� | $\frac{4��R}{T}$ | C�� | $\frac{10��R}{T}$ | D�� | $\frac{25��R}{T}$ |
| A�� | 1�� | B�� | 2�� | C�� | 4�� | D�� | 8�� |
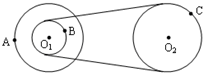 ��ͼ��ʾ��Ƥ������װ���У���A��Bͬ�ᣬa��b��c�ֱ��������ֱ�Ե����Ϊ1kg��1kg��2kg��Բ��һ���˶���С��飬��RA=RC=2RB����a��b��c��������ֵ�Ħ��ϵ���ֱ�Ϊ0.4��0.3��0.3������С����Ħ����֮���ǣ�������
��ͼ��ʾ��Ƥ������װ���У���A��Bͬ�ᣬa��b��c�ֱ��������ֱ�Ե����Ϊ1kg��1kg��2kg��Բ��һ���˶���С��飬��RA=RC=2RB����a��b��c��������ֵ�Ħ��ϵ���ֱ�Ϊ0.4��0.3��0.3������С����Ħ����֮���ǣ�������| A�� | 4��2��1 | B�� | 2��1��1 | C�� | 1��2��4 | D�� | 4��3��6 |
| A�� | vm��Ϊ����ֵ����al��a2�Ĵ�С�й� | B�� | vmֻ��Ϊ2V����a1��a2�Ĵ�С�� | ||
| C�� | a1��a2��������$\frac{{a}_{1}{a}_{2}}{{a}_{1}+{a}_{2}}$=$\frac{2v}{t}$ | D�� | a1��a2��������$\frac{2{a}_{1}{a}_{2}}{{a}_{1}+{a}_{2}}$=$\frac{v}{t}$ |
| A�� | �����˶�������Ϊ$v=e\sqrt{\frac{k}{mr}}$ | B�� | �����˶�������Ϊ$T=\frac{2��r}{e}\sqrt{\frac{m}{k}}$ | ||
| C�� | �����˶��γɵĵ���$I=\frac{e^2}{2��r}\sqrt{\frac{k}{mr}}$ | D�� | �����˶��γɵĵ���$I=\frac{{{e^{\;}}}}{2��r}\sqrt{\frac{k}{mr}}$ |
| A�� | 4sĩ | B�� | 2sĩ | C�� | 6sĩ | D�� | 24sĩ |
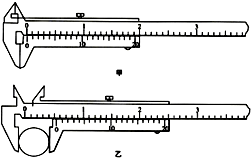 ijͬѧ�����α꿨�߲���һ����ԲͲ���⾶��ͼ��Ϊ���α꿨��У��ʱ��ʾ����ͼ��Ϊ��������ԲͲ�⾶ʱ��ʾ������ͼ����ʾ������Ϊ0.15mm����ͼ����ʾ������Ϊ5.35mm���������Ͳ�⾶Ϊ5.20mm��
ijͬѧ�����α꿨�߲���һ����ԲͲ���⾶��ͼ��Ϊ���α꿨��У��ʱ��ʾ����ͼ��Ϊ��������ԲͲ�⾶ʱ��ʾ������ͼ����ʾ������Ϊ0.15mm����ͼ����ʾ������Ϊ5.35mm���������Ͳ�⾶Ϊ5.20mm�� ��ͼ��ʾΪ��ŷķ��ԭ��ʾ��ͼ�����е���������ƫ����Ig=100��A������Rg=100�����ɱ����R�������ֵΪ10k������صĵ綯��E=1.5V������r=0.5����ͼ���������B�����ı�����ɫӦ�Ǻ�ɫ������ȷʹ�÷�����������Rx����ֵʱ��ָ��ָ�ڿ̶��̵������룬��Rx=15k����
��ͼ��ʾΪ��ŷķ��ԭ��ʾ��ͼ�����е���������ƫ����Ig=100��A������Rg=100�����ɱ����R�������ֵΪ10k������صĵ綯��E=1.5V������r=0.5����ͼ���������B�����ı�����ɫӦ�Ǻ�ɫ������ȷʹ�÷�����������Rx����ֵʱ��ָ��ָ�ڿ̶��̵������룬��Rx=15k����