题目内容
17.以速度v0水平抛出一小球,抛出后某时刻小球的竖直分位移与水平分位移大小相等,以下判断正确的是( )| A. | 此时小球的竖直分速度大小等于水平分速度大小 | |
| B. | 此时小球的速度大小为$\sqrt{2}$v0 | |
| C. | 小球从抛出到达此位置的时间为$\frac{{2{v_0}}}{g}$ | |
| D. | 此时小球的速度方向与位移方向相同 |
分析 通过竖直分位移与水平分位移大小相等,求出时间,根据时间可求出竖直方向的分速度以及速度的大小和方向.
解答 解:A、根据$\frac{1}{2}g{t}^{2}={v}_{0}t$得,小球的运动时间t=$\frac{2{v}_{0}}{g}$,则竖直分速度vy=gt=2v0,与水平分速度不等,故A错误,C正确.
B、根据平行四边形定则知,小球的速度大小v=$\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=\sqrt{{{v}_{0}}^{2}+4{{v}_{0}}^{2}}=\sqrt{5}{v}_{0}$,故B错误.
D、速度方向与水平方向夹角正切值$tanα=\frac{{v}_{y}}{{v}_{0}}=2$,位移与水平方向夹角的正切值$tanθ=\frac{y}{x}=1$,故D错误.
故选:C.
点评 解决本题的关键掌握处理平抛运动的方法,平抛运动可分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动.且分运动与合运动具有等时性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.关于电磁波的应用,下列说法正确的是( )
| A. | 医院里常用X射线对手术室进行消毒 | |
| B. | 工业上利用γ射线检查金属内部有无沙眼 | |
| C. | 利用红外线遥感技术在卫星上监测森林火情 | |
| D. | 利用紫外线烘干谷物 |
5.氢原子的部分能级如图所示.已知可见光的光子能量在1.62eV到3.11eV之间.由此可推知,氢原子( )
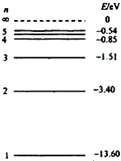

| A. | 从高能级向n=1能级跃迁时发出的光的波长比可见光的短 | |
| B. | 从高能级向n=2能级跃迁时发出的光均为可见光 | |
| C. | 从高能级向n=3能级跃迁时发出的光的频率比可见光的高 | |
| D. | 从n=2能级向n=1能级跃迁时发出的光为可见光 |
12.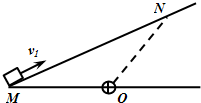 如图所示,粗糙程度均匀的绝缘斜面下方O点处有一正点电荷,带负电的小物体以初速度v1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为v2(v2<v1).若小物体电荷量保持不变,OM=ON,则
如图所示,粗糙程度均匀的绝缘斜面下方O点处有一正点电荷,带负电的小物体以初速度v1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为v2(v2<v1).若小物体电荷量保持不变,OM=ON,则
( )
 如图所示,粗糙程度均匀的绝缘斜面下方O点处有一正点电荷,带负电的小物体以初速度v1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为v2(v2<v1).若小物体电荷量保持不变,OM=ON,则
如图所示,粗糙程度均匀的绝缘斜面下方O点处有一正点电荷,带负电的小物体以初速度v1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为v2(v2<v1).若小物体电荷量保持不变,OM=ON,则( )
| A. | 小物体上升的最大高度为$\frac{v_1^2-v_2^2}{4g}$ | |
| B. | 从N到M的过程中,小物体的电势能逐渐减小 | |
| C. | 从M到N的过程中,电场力对小物体先做负功后做正功 | |
| D. | 从N到M的过程中,小物体受到的摩擦力和电场力均是先增大后减小 |
9.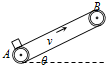 某机场利用如图所示的传送带将地面上的货物运送到飞机上,传送带与地面的夹角θ=30°传送带两端A、B的长度L=10m.传送带以v=5m/s的恒定速度匀速向上运动.在传送带底端A轻轻放一质量m=5kg的货物,货物与传送带间的动磨擦因数为$\frac{\sqrt{3}}{2}$,g取10m/s2.( )
某机场利用如图所示的传送带将地面上的货物运送到飞机上,传送带与地面的夹角θ=30°传送带两端A、B的长度L=10m.传送带以v=5m/s的恒定速度匀速向上运动.在传送带底端A轻轻放一质量m=5kg的货物,货物与传送带间的动磨擦因数为$\frac{\sqrt{3}}{2}$,g取10m/s2.( )
 某机场利用如图所示的传送带将地面上的货物运送到飞机上,传送带与地面的夹角θ=30°传送带两端A、B的长度L=10m.传送带以v=5m/s的恒定速度匀速向上运动.在传送带底端A轻轻放一质量m=5kg的货物,货物与传送带间的动磨擦因数为$\frac{\sqrt{3}}{2}$,g取10m/s2.( )
某机场利用如图所示的传送带将地面上的货物运送到飞机上,传送带与地面的夹角θ=30°传送带两端A、B的长度L=10m.传送带以v=5m/s的恒定速度匀速向上运动.在传送带底端A轻轻放一质量m=5kg的货物,货物与传送带间的动磨擦因数为$\frac{\sqrt{3}}{2}$,g取10m/s2.( )| A. | 货物从A到B过程中摩擦力不变 | B. | 货物从A到B的时间为3s | ||
| C. | 货物传送带上滑动的时间为2s | D. | 货物相对传送带滑动的距离为5m |
6.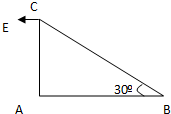 如图,A、B、C三点为一直角三角形的三个顶点,∠B=30°,现在A、B两点放置两点电荷qA、qB,测得C点场强方向与BA平行,则关于qA、qB的电性及其大小关系,下列说法中正确的是( )
如图,A、B、C三点为一直角三角形的三个顶点,∠B=30°,现在A、B两点放置两点电荷qA、qB,测得C点场强方向与BA平行,则关于qA、qB的电性及其大小关系,下列说法中正确的是( )
 如图,A、B、C三点为一直角三角形的三个顶点,∠B=30°,现在A、B两点放置两点电荷qA、qB,测得C点场强方向与BA平行,则关于qA、qB的电性及其大小关系,下列说法中正确的是( )
如图,A、B、C三点为一直角三角形的三个顶点,∠B=30°,现在A、B两点放置两点电荷qA、qB,测得C点场强方向与BA平行,则关于qA、qB的电性及其大小关系,下列说法中正确的是( )| A. | qA一定带正电 | B. | qB一定带正电 | C. | qA:qB=1:4 | D. | qA:qB=1:8 |
7.简谐横波某时刻的波形图线如图所示,a为介质中的一个质点,由图象可知( )
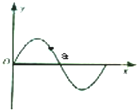

| A. | 此时质点a的加速度方向一定沿y轴负方向 | |
| B. | 此时质点a的速度方向一定沿y轴负方向 | |
| C. | 若波向左传播,则此时a的速度方向一定沿y轴负方向 | |
| D. | 若波向右传播,则此时a的速度方向一定沿y轴负方向 |
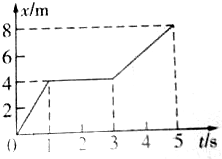 一质点做直线运动的x-t图象如图所示,则在0-1s,1-3s,3-5s时间内质点做什么运动?t=0.5s、t=2.5s和t=3.5s时,质点的速度为多大?
一质点做直线运动的x-t图象如图所示,则在0-1s,1-3s,3-5s时间内质点做什么运动?t=0.5s、t=2.5s和t=3.5s时,质点的速度为多大?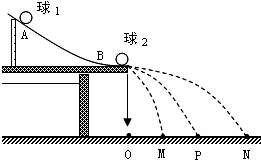 在实验中使用半径相等的钢质小球1和2验证动量守恒如图,实验步骤如下:
在实验中使用半径相等的钢质小球1和2验证动量守恒如图,实验步骤如下: