题目内容
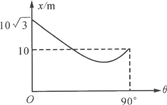
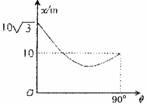
物体从斜面底部以一定的速率沿斜面向上运动,斜面底边水平,倾角可在0°~90°之间变化,物体沿斜面到达的最远距离x和倾角θ的关系如图所示,求:
(1)物体与接触面的动摩擦因数;
(2)θ为多大时,x有最小值,并求出最小值.
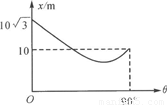
【答案】分析:(1)物体沿斜面向上做匀减速直线运动,由牛顿第二定律和运动学结合,分别得出0°和90°时物体沿斜面上升的最大位移s与斜面倾角θ的关系表达式,即可求出动摩擦因数;
(2)由动能定理得到x与θ的关系式,运用数学知识求解最小值及达到最小值的条件.
解答:解:(1)设初速度为v,当θ=0°时,物体沿水平方向运动,故
μmg=ma ①
v2=2aSx ②
当θ=90°时,物体沿竖直方向做上抛运动,故
v2=2gh ③
联立①、②、③解得:μ=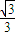 ④
④
(2)当物体以任意角运动时,由动能定理得
-μmgxsinθ-μmgxcosθ=0-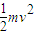 ⑤
⑤
联立①、②、③、⑤解得:x= ⑥
⑥
可见,当θ=60°时,x有最小值:xmin=5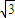 ⑦
⑦
答:
(1)物体与接触面的动摩擦因数为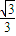 ;
;
(2)θ为60°时,x有最小值,最小值为5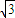 .
.
点评:本题关键是根据动能定理求出位移的一般表达式,然后结合图象求出初速度和动摩擦因素,再用解析法求出位移的最小值.
(2)由动能定理得到x与θ的关系式,运用数学知识求解最小值及达到最小值的条件.
解答:解:(1)设初速度为v,当θ=0°时,物体沿水平方向运动,故
μmg=ma ①
v2=2aSx ②
当θ=90°时,物体沿竖直方向做上抛运动,故
v2=2gh ③
联立①、②、③解得:μ=
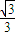 ④
④(2)当物体以任意角运动时,由动能定理得
-μmgxsinθ-μmgxcosθ=0-
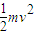 ⑤
⑤联立①、②、③、⑤解得:x=
 ⑥
⑥可见,当θ=60°时,x有最小值:xmin=5
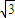 ⑦
⑦答:
(1)物体与接触面的动摩擦因数为
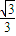 ;
;(2)θ为60°时,x有最小值,最小值为5
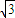 .
.点评:本题关键是根据动能定理求出位移的一般表达式,然后结合图象求出初速度和动摩擦因素,再用解析法求出位移的最小值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
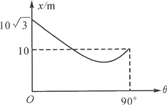 (2007?茂名一模)物体从斜面底部以一定的速率沿斜面向上运动,斜面底边水平,倾角可在
(2007?茂名一模)物体从斜面底部以一定的速率沿斜面向上运动,斜面底边水平,倾角可在